Câu hỏi
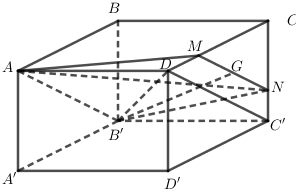
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(AB = 3a,AD = 4a,AA' = 4a\). Gọi \(G\) là trọng tâm tam giác \(CC'D\). Mặt phẳng chứa \(B'G\) và song song với \(C'D\) chia khối hộp thành \(2\) phần. Gọi \(\left( H \right)\) là khối đa diện chứa \(C\). Tính tỉ số \(\frac{{{V_{\left( H \right)}}}}{V}\) với \(V\) là thể tích khối hộp đã cho.
- A \(\frac{{19}}{{54}}\)
- B \(\frac{{38}}{3}\)
- C \(\frac{{23}}{4}\)
- D \(\frac{{25}}{2}\)
Phương pháp giải:
- Dựng mặt phẳng chứa \(B'G\) và song song \(C'D\).
- Xác định khối đa diện và tính thể tích bằng cách cộng trừ thể tích các khối đa diện đơn giản.
Lời giải chi tiết:
Gọi \(\left( \alpha \right)\) là mặt phẳng chứa \(B'G\) và song song với \(C'D.\)
Gọi \(M,\,N\) lần lượt là giao điểm của \(\left( \alpha \right)\) với \(CD\) và \(CC'.\)
Khi đó ta có: \(MN//C'D\) và \(\frac{{CM}}{{CD}} = \frac{{CN}}{{CC'}} = \frac{2}{3}\)
Và \(\left( \alpha \right)\) là mặt phẳng \(\left( {AMNB'} \right),\,\,\left( H \right)\) là phần khối đa diện chứa \(C.\)
Khi đó ta có: \({V_{\left( H \right)}} = {V_{M.BCNB'}} + {V_{B'.ABM}}\)
Ta có: \(BCNB'\) là hình thang vuông tại \(B,\,\,C\) có diện tích:
\(\begin{array}{l}{S_{BCNB'}} = \frac{1}{2}\left( {BB' + CN} \right).BC = \frac{1}{2}\left( {4a + \frac{2}{3}.4a} \right).4a = \frac{{40{a^2}}}{3}.\\ \Rightarrow {V_{MBCNB'}} = \frac{1}{3}MC.{S_{BCNB'}} = \frac{1}{3}.\frac{2}{3}.3a.\frac{{40}}{3}{a^2} = \frac{{80{a^3}}}{9}.\end{array}\)
Mặt khác \({S_{\Delta ABM}} = {S_{ABCD}} - {S_{\Delta BCM}} - {S_{\Delta ADM}} = 3a.4a - \frac{1}{2}.4a.\frac{2}{3}.3a - \frac{1}{2}.4a.\frac{1}{3}.3a = 6{a^2}.\)
\(\begin{array}{l} \Rightarrow {V_{B'ABM}} = \frac{1}{3}BB'.{S_{ABM}} = \frac{1}{3}.4a.6{a^2} = 8{a^3}.\\ \Rightarrow {V_{\left( H \right)}} = \frac{{80}}{9}{a^3} + 8{a^3} = \frac{{152{a^3}}}{9}.\end{array}\)
Thể tích hình hộp chữ nhật là: \(V = 3a.4a.4a = 48{a^3}.\)
\( \Rightarrow \frac{{{V_{\left( H \right)}}}}{V} = \frac{{152{a^3}}}{9}.\frac{1}{{48{a^3}}} = \frac{{19}}{{54}}.\)
Chọn A.