Câu hỏi
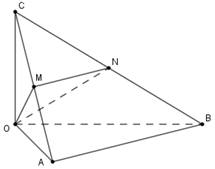
Cho khối tứ diện \(OABC\) với \(OA,OB,OC\) vuông góc từng đôi một và \(OA = a;OB = 2a;OC = 3a.\) Gọi \(M,N\) lần lượt là trung điểm của hai cạnh \(AC,BC.\) Thể tích của khối tứ diện \(OCMN\) theo \(a\) bằng
- A \(\frac{{{a^3}}}{4}\)
- B \({a^3}\)
- C \(\frac{{3{a^3}}}{4}\)
- D \(\frac{{2{a^3}}}{3}\)
Phương pháp giải:
Sử dụng công thức tính thể tích khối chóp có chiều cao \(h\) và diện tích đáy \(S\) là \(V = \frac{1}{3}h.S\)
Sử dụng công thức tỉ lệ thể tích : Cho hình chóp \(S.ABC\) có \(M,N,P\) lần lượt thuộc các cạnh \(SA,SB,SC\). Khi đó ta có \(\frac{{{V_{S.MNP}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SB}}.\frac{{SP}}{{SC}}\)
Lời giải chi tiết:
Ta có \({V_{OABC}} = \frac{1}{3}OA.{S_{OBC}} = \frac{1}{3}.a.\frac{1}{2}.2a.3a = {a^3}\)
Lại có \(\frac{{{V_{OCMN}}}}{{{V_{OCAB}}}} = \frac{{OC}}{{OC}}.\frac{{OM}}{{OA}}.\frac{{ON}}{{OB}} = \frac{1}{2}.\frac{1}{2} = \frac{1}{4}\) nên \({V_{OCMN}} = \frac{1}{4}{V_{OCAB}} = \frac{1}{4}.{a^3} = \frac{{{a^3}}}{4}\)
Chọn A.