Môn Lý - Lớp 12
Môn Lý - Lớp 12
 50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng (Phần 2)
50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng (Phần 2)
Câu hỏi
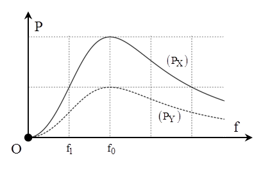
Đoạn mạch gồm hai hộp kín X và Y mắc nối tiếp, mỗi hộp chứa hai trong ba phần tử mắc nối tiếp, điện trở thuần, cuộn cảm thuần, tụ điện. Đặt vào hai đầu đoạn mạch một hiệu điện thế xoay chiều u = U0cos2πft, U0 không đổi, f thay đổi được. Cho f thay đổi thu được đồ thị sự phụ thuộc của công suất tỏa nhiệt trên hộp X (Px) và hộp Y (Py) theo f như hình vẽ. Khi f = f1 thì góc lệch pha giữa hiệu điện thế hai đầu hộp X (ux) và Y (uY) gần với giá trị nào nhất sau đây? Biết uX chậm pha hơn uY
- A 1200
- B 1000
- C 1300
- D 1100
Phương pháp giải:
Mạch xảy ra cộng hưởng khi ZL = ZC
Công suất tiêu thụ P = I2R
ĐỊnh luật Ôm cho đoạn mạch: I = U/Z
Tổng trở mạch RLC là \(Z=\sqrt{{{R}^{2}}+{{({{Z}_{L}}-{{Z}_{C}})}^{2}}}\)
Mạch chứa R có u cùng pha i, mạch chỉ chứa L có u sớm pha π/2 so với i, mạch chỉ chứa C có u chậm pha π/2 so với i.
Lời giải chi tiết:
Vì uX trễ pha hơn uY nên X chứa RX và ZC, Y chứa RY và ZL
Từ đồ thị ta thấy khi f = f0 mạch xảy ra cộng hưởng, ZL0 = ZC0
Chuẩn hóa ZL0 = ZC0 = 1
Pxmax = 2PYmax => RX = 2RY
Khi f = f1 = 0,5f0 thì ZL1 = 0,5ZL0 = 0,5; ZC1 = 2ZC0 = 2
Mặt khác PX = PYmax => \(\frac{{{U}^{2}}{{R}_{x}}}{{{({{R}_{X}}+{{R}_{Y}})}^{2}}+{{({{Z}_{L1}}-{{Z}_{C1}})}^{2}}}=\frac{{{U}^{2}}{{R}_{Y}}}{{{({{R}_{X}}+{{R}_{Y}})}^{2}}}\Rightarrow \frac{2}{9R_{Y}^{2}+{{(0,5-2)}^{2}}}=\frac{1}{9R_{Y}^{2}}\)
=> RY = 0,5; RX = 1
=> Độ lệch pha giữa uYvà uX là
\(\Delta \varphi =\arctan \frac{{{Z}_{C1}}}{{{R}_{X}}}+\arctan \frac{{{Z}_{L1}}}{{{R}_{Y}}}=\arctan \frac{2}{1}+\arctan \frac{0,5}{0,5}={{108}^{0}}\)
Chọn D