Phương pháp giải:

Nhận xét tính chất của đường thẳng \(y = m\) dựa vào điều kiện tiếp xúc với đồ thị hàm số tại hai điểm phân biệt.

Lời giải chi tiết:

Đồ thị hàm số \(\left( C \right)\) có dạng:

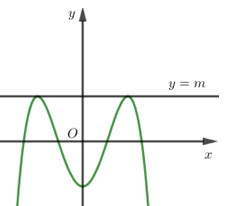
Quan sát dáng đồ thị ta thấy, nếu đường thẳng \(y = m\) tiếp xúc với đồ thị hàm số \(\left( C \right)\) tại hai điểm phân biệt thì chúng phải là hai điểm cực đại của đồ thị hàm số.

Hàm số \(y =  - 2{x^4} + 4{x^2} - 1\) có \(y' =  - 8{x^3} + 8x = 8x\left( { - {x^2} + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y =  - 1\\x =  \pm 1 \Rightarrow y = 1\end{array} \right.\)

Vậy hai điểm cực đại của đồ thị hàm số là \(A\left( {1;1} \right)\) và \(B\left( { - 1;1} \right)\).

Vậy \({y_A} + {y_B} = 2\).

Chọn A.