Câu hỏi
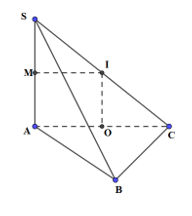
Cho hình chóp \(S.ABC\) có đáy là tam giác ABC vuông cân tại B, \(AB = a,\,\,SA = 2a,\,\,SA \bot \left( {ABC} \right)\). Bán kính của mặt cầu ngoại tiếp hình chóp \(S.ABC\) là:
- A \(\dfrac{{a\sqrt 6 }}{2}\).
- B \(\dfrac{{a\sqrt 6 }}{6}\).
- C \(\dfrac{{a\sqrt 3 }}{2}\).
- D \(\dfrac{{a\sqrt 6 }}{3}\).
Phương pháp giải:
Cách xác định tâm mặt cầu ngoại tiếp khối chóp:
- Xác định tâm O của đường tròn ngoại tiếp đa giác đáy
- Từ O dựng đường thẳng d vuông góc với mặt phẳng đáy
- Dựng mặt phẳng trung trực \(\left( \alpha \right)\)của một cạnh bên nào đó
- Xác định \(I = \left( \alpha \right) \cap d\), I chính là tâm mặt cầu ngoại tiếp hình chóp đã cho.
Lời giải chi tiết:
Gọi O, I lần lượt là trung điểm của AC, SC.
Ta có:
\(\Delta \)ABC vuông cân tại B \( \Rightarrow O\) là tâm đường tròn ngoại tiếp và \(AC = AB.\sqrt 2 = a\sqrt 2 \).
Mà \(OI//SA,\,\,SA \bot \left( {ABC} \right) \Rightarrow OI \bot \left( {ABC} \right) \Rightarrow IA = IB = IC\)(1)
\(\Delta \)SAC vuông tại A, I là trung điểm của SC \( \Rightarrow IS = IC = IA\) (2)
Từ (1), (2) suy ra \(I\) là tâm mặt cầu ngoại tiếp hình chóp S.ABC, bán kính \(R = \dfrac{{SC}}{2} = \dfrac{{\sqrt {S{A^2} + A{C^2}} }}{2} = \dfrac{{\sqrt {{{\left( {2a} \right)}^2} + {{\left( {a\sqrt 2 } \right)}^2}} }}{2} = \dfrac{{a\sqrt 6 }}{2}\).
Chọn: A