Câu hỏi
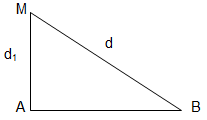
Trên bề mặt chất lỏng có hai nguồn kết hợp A, B cách nhau 12cm dao động cùng pha Biết sóng do mỗi nguồn phát ra có tần cố f = 10Hz, vận tốc truyền sóng 40cm/s. Gọi M là một điểm nằm trên đường vuông góc với AB qua A và tại đó M dao động với biên độ cực đại. Đoạn AM có giá trị lớn nhất là:
- A 20cm.
- B 24cm.
- C 16cm.
- D 12cm.
Phương pháp giải:
Điều kiện có cực đại giao thoa sóng hai nguồn cùng pha
Lời giải chi tiết:
+ Bước sóng λ = v/f = 40/10 = 4 cm.
+ Điểm M nằm trên đường thẳng vuông góc với AB tại A đồng thời thỏa mãn hai điều kiện dao động với biên độ cực đại và xa A nhất => M thuộc đường cực đại ứng với k = 1
Hay d2 – d1 = λ = 4 cm(1)
Mặt khác ta có: \(d_2^2 - d_1^2 = A{B^2} = > {d_2} + {d_1} = {{A{B^2}} \over {{d_2} - {d_1}}} = {{{{12}^2}} \over 4} = 36\) (2)
Giải (1) và (2) ta được AM = d1 = 16 cm
=> Chọn C
Câu hỏi trước
