Câu hỏi
Một sợi dây đàn hồi AB được căng thao phương ngang. Đầu B cố đinh. Đầu A gắn với cần rung có tần số 200 HZ, tạo ra sóng dừng trên dây. Biết tốc độ truyền sóng trên dây là 24 m/s. Biên độ dao động cuả bụng là 4cm. Trên dây, M là một nút. Gọi N, P, Q là các điểm trên sợi dây, nằm cùng một phía với M và có vị trí cân bằng cách M lần lượt là 2 cm, 8 cm và 10 cm. Khi có sóng dừng, diện tích lớn nhất của tứ giác MNPQ có giá trị gần nhất với giá trị nào sau đây?
- A 16 cm2
- B 49 cm2
- C 28 cm2
- D 23 cm2
Phương pháp giải:
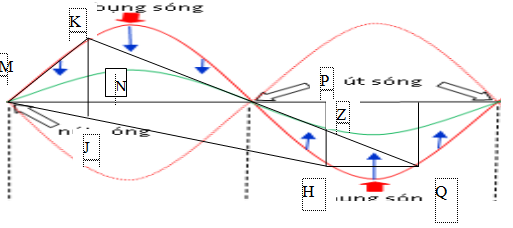
Vẽ hình vẽ biểu diễn các vị trí các điểm
Dựa vào hình học xác định diện tích. Hình tứ giác có diện tích lớn nhất khi các điểm ở vị trí biên.
Lời giải chi tiết:
Bước sóng:
\(\lambda = \frac{v}{f} = \frac{{2400}}{{200}} = 12cm\)
Biên độ bụng sóng A = 2a = 4 cm.
Ta có các vị trí các điểm so với nút M: N: 2 cm = λ/6
P: 8 cm = 2λ/3
Q: 10 cm = 5λ/6.
Diện tích MNPQ lớn nhất khi các điểm N, P, Q ở biên.
S = S1 + S2 + S3
S1 = ½. MN. KJ
S2= (KJ+ ZH). NP/2 = \(2a\sqrt 3 .\frac{\lambda }{{2.2}} = \frac{{a\sqrt 3 .\lambda }}{2} = 20,78c{m^2}\)
S3 = ½. PQ. HZ
S1 + S3 = ½. MN. 2a = 6,92 cm2
Chọn D. 23 cm2