Câu hỏi
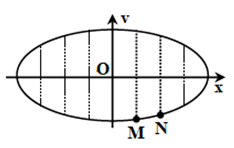
Một vật dao động điều hòa. Hình bên là đồ thị biểu diễn mối quan hệ giữa vận tốc v và li độ x của vật. Gọi k1 và k2 lần lượt là hệ số góc của tiếp tuyến với đồ thị tại M và N. tỷ số \(\frac{{{k_1}}}{{{k_2}}}\) bằng
- A \(\frac{1}{{\sqrt 5 }}\)
- B \(\frac{2}{{\sqrt 7 }}\)
- C \(\frac{1}{{\sqrt 6 }}\)
- D \(\frac{2}{{\sqrt 5 }}\)
Phương pháp giải:
Phương trình độc lập với thời gian: \({x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2}\)
Lời giải chi tiết:
Dễ thấy \({x_M} = \frac{A}{4};{x_N} = \frac{A}{2}\)
Phương trình độc lập với thời gian:
\(\begin{array}{l}
{x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Leftrightarrow {v^2} = {\omega ^2}.({A^2} - {x^2})\\
\Rightarrow 2v.dv = - 2{\omega ^2}.x.dx\\
\Rightarrow \frac{{dv}}{{dx}} = \frac{{ - {\omega ^2}.x}}{v}
\end{array}\)
Tỉ số:
\(\frac{{{k_1}}}{{{k_2}}} = \frac{{\frac{{d{v_1}}}{{d{x_1}}}}}{{\frac{{d{v_2}}}{{d{x_2}}}}} = \frac{{{x_1}}}{{{x_2}}}.\frac{{{v_2}}}{{{v_1}}} = \frac{1}{2}.\frac{{{v_2}}}{{{v_1}}}\)
Thay các giá trị x vào phương trình độc lập với thời gian ta tìm được :
\(\begin{array}{l}
{v_1}^2 = {\omega ^2}.({A^2} - {x_1}^2) = {\omega ^2}.({A^2} - {\frac{A}{{16}}^2}) = \frac{{15}}{{16}}{\omega ^2}.{A^2}\\
{v_2}^2 = {\omega ^2}.({A^2} - {x_2}^2) = {\omega ^2}.({A^2} - {\frac{A}{4}^2}) = \frac{3}{4}{\omega ^2}.{A^2}\\
\Rightarrow \frac{{{v_2}}}{{{v_1}}} = \sqrt {\frac{4}{5}} = \frac{2}{{\sqrt 5 }}
\end{array}\)
Suy ra: \(\frac{{{k_1}}}{{{k_2}}} = \frac{1}{2}.\frac{2}{{\sqrt 5 }} = \frac{1}{{\sqrt 5 }}\)
Chọn A.