Câu hỏi
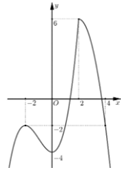
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Có bao nhiêu số nguyên \(m\) để phương trình \(\frac{1}{3}f\left( {\frac{x}{2} + 1} \right) + x = m\) có nghiệm thuộc đoạn \(\left[ { - 2;\,2} \right]?\)
- A \(11\)
- B \(9\)
- C \(8\)
- D \(10\)
Phương pháp giải:
+) Đặt \(t = \frac{x}{2} + 1\). Đưa phương trình về dạng \(g\left( t \right) = m,\,\,t \in \left[ {a;b} \right]\).
+) Phương trình có nghiệm \( \Leftrightarrow t \in \left[ {\mathop {\min }\limits_{\left[ {a;b} \right]} g\left( t \right);\mathop {\max }\limits_{\left[ {a;b} \right]} g\left( t \right)} \right]\).
Lời giải chi tiết:
Đặt \(t = \frac{x}{2} + 1,\,\,x \in \left[ { - 2;2} \right] \Rightarrow t \in \left[ {0;2} \right]\) và \(x = 2\left( {t - 1} \right)\).
Khi đó ta có \(\frac{1}{3}f\left( t \right) + 2\left( {t - 1} \right) = m,\,\,t \in \left[ {0;2} \right] \Leftrightarrow f\left( t \right) = 3m - 6\left( {t - 1} \right) = - 6t + 3m + 6\,\,\left( * \right)\).
Số nghiệm của (*) là số giao điểm của đồ thị hàm số \(y = f\left( t \right)\) và đường thẳng \(\left( d \right):\,\,y = - 6t + 3m + 6\)
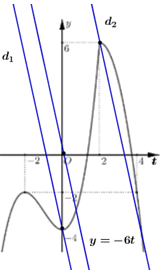
Vẽ đồ thị hàm số \(y = f\left( t \right)\) và \(y = - 6t\) trên cùng 1 mặt phẳng tọa độ ta có :
Gọi \({d_1}\) là đường thẳng đi qua \(\left( {0; - 4} \right)\) và song song với đường thẳng \(y = - 6t \Rightarrow \left( {{d_1}} \right):\,\,y = - 6t - 4\)
Gọi \({d_1}\) là đường thẳng đi qua \(\left( {2;5} \right)\) và song song với đường thẳng \(y = - 6t \Rightarrow \left( {{d_2}} \right):\,\,y = - 6t + 17\).
Để phương trình (*) có nghiệm \(t \in \left[ {0;2} \right] \Rightarrow \) Đường thẳng \(\left( d \right):\,\,y = - 6t + 3m + 6\) nằm giữa hai đường thẳng \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) \( \Rightarrow - 4 \le 3m + 6 \le 17 \Leftrightarrow - \frac{{10}}{3} \le m \le \frac{{11}}{3}\).
Kết hợp điều kiện \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 3; - 2; - 1;0;1;2;3} \right\}\).
Vậy có 7 giá trị của \(m\) thỏa mãn yêu cầu bài toán.
KHÔNG CÓ ĐÁP ÁN.