Lời giải chi tiết:

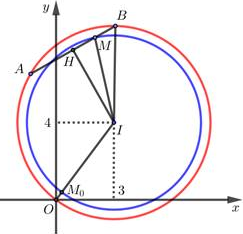
Giả sử \(z = x + yi\). Gọi \(A,\,\,B\) lần lượt là các điểm biểu diễn cho số phức \({z_1},\,\,{z_2}\) ta có \(AB = 4\).

Ta có:

\(\begin{array}{l}\left( {z - 6} \right)\left( {8 + \overline {zi} } \right) = \left( {x + yi - 6} \right)\left( {8 + \overline {\left( {x + yi} \right)i} } \right) = \left[ {\left( {x - 6} \right) + yi} \right]\left( {8 - xi - y} \right)\\ = \left[ {\left( {x - 6} \right) + yi} \right]\left[ {\left( {8 - y} \right) - xi} \right] = \left( {x - 6} \right)\left( {8 - y} \right) + xy + \left[ {\left( {8 - y} \right)y - \left( {x + 6} \right)x} \right]i\\ = 8x - xy - 48 + 6y + xy - \left( {{x^2} + {y^2} + 6x - 8y} \right)i\\ = 8x + 6y - 48 - \left( {{x^2} + {y^2} + 6x - 8y} \right)i\end{array}\)

Theo bài ra ta có \({x^2} + {y^2} - 6x - 8y = 0\).

\( \Rightarrow A,B \in \left( C \right):\,\,{x^2} + {y^2} - 6x - 8y = 0\) là đường tròn tâm \(\left( {4;3} \right)\) bán kính \(R = 5\).

Xét điểm \(M\) thỏa mãn \(\overrightarrow {MA}  + 3\overrightarrow {MB}  = \overrightarrow 0 \)

\( \Leftrightarrow \overrightarrow {MO}  + \overrightarrow {OA}  + 3\overrightarrow {MO}  + \overrightarrow {OB}  = \overrightarrow 0  \Leftrightarrow \overrightarrow {OA}  + 3\overrightarrow {OB}  = 4\overrightarrow {OM} \)

Gọi \(H\) là trung điểm của \(AB\) ta có : \(H{I^2} = {R^2} - H{B^2} = 21,\,\,IM = \sqrt {H{I^2} + H{M^2}}  = \sqrt {22} \).

\( \Rightarrow \) M thuộc đường tròn \(\left( T \right)\) tam \(I\left( {3;4} \right)\) bán kính \(R' = \sqrt {22} \).

Ta có : \(\left| {{z_1} + 3{z_2}} \right| = \left| {\overrightarrow {OA}  + 3\overrightarrow {OB} } \right| = \left| {4\overrightarrow {OM} } \right| = 4OM\)

\( \Rightarrow {\left| {{z_1} + 3{z_2}} \right|_{\min }} \Leftrightarrow O{M_{\min }} = \left| {OI - R'} \right| = 5 - \sqrt {22} \).

Vậy \({\left| {{z_1} + 3{z_2}} \right|_{\min }} = 4\left( {5 - \sqrt {22} } \right) = 20 - 4\sqrt {22} \).

Chọn C.