Phương pháp giải:

Tập hợp các điểm biểu diễn của các số phức thỏa mãn \(\left| {z - a - bi} \right| = R,\,\,R > 0\) là đường tròn: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\).

Lời giải chi tiết:

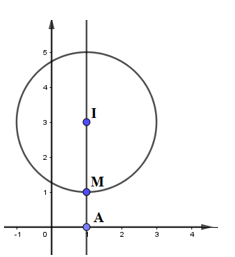
Tập hợp các điểm M biểu diễn của các số phức thỏa mãn \(\left| {z - 1 - 3i} \right| = 2\) là đường tròn: \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 4\)

 là khoảng cách từ điểm M đến điểm \(A\left( {1;0} \right)\). Khoảng cách này nhỏ nhất khi và chỉ khi M nằm giữa I và A (với \(I\left( {1;3} \right)\) là tâm đường tròn \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 4\))

 Dễ dàng tính được \(M\left( {1;1} \right)\).

Vậy, số phức z thỏa mãn là \(z = 1 + i\).

Chọn: B