Câu hỏi
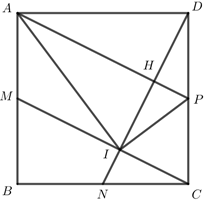
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD; các điểm M, N, P lần lượt là trung điểm của AB, BC và CD; CM cắt DN tại điểm \(I\left( {5;\,2} \right)\). Biết \(P\left( {\frac{{11}}{2};\frac{{11}}{2}} \right)\) và điểm A có hoành độ âm.
Câu 1: Viết phương trình tổng quát đường thẳng đi qua hai điểm I, P.
- A \(7x - y - 33 = 0\)
- B \(7x + y + 33 = 0\)
- C \(7x + y - 33 = 0\)
- D \(7x - y + 33 = 0\)
Phương pháp giải:
Phương trình tổng quát của đường thẳng \(\Delta \) đi qua \(A\left( {{x_0};{y_0}} \right)\) có VTPT \(\overrightarrow n = \left( {a;b} \right)\) là: \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\)
Lời giải chi tiết:
Ta có: \(\overrightarrow {IP} = \left( {\frac{1}{2};\frac{7}{2}} \right) = \frac{1}{2}\left( {1;\;7} \right).\)
Đường thẳng IP nhận \(\overrightarrow {IP} \) là một VTCP \( \Rightarrow \overrightarrow n = \left( {7; - 1} \right)\) là một VTPT của IP
\( \Rightarrow \) Phương trình IP: \(7\left( {x - 5} \right) - \left( {y - 2} \right) = 0 \Leftrightarrow 7x - y - 33 = 0\)
Chọn A.
Câu 2: Tìm tọa độ điểm A và D.
- A \(A\left( {2;3} \right),\,\,D\left( { - 3;8} \right)\)
- B \(A\left( {2;-3} \right),\,\,D\left( { - 3;8} \right)\)
- C \(A\left( { - 2; - 3} \right),\,\,D\left( {3; - 8} \right)\)
- D \(A\left( { - 2;3} \right),\,\,D\left( {3;8} \right)\)
Phương pháp giải:
Sử dụng tính chất trung điểm.
Lời giải chi tiết:
Gọi H là giao điểm của AP với DN
Dễ chứng minh được \(CM \bot DN\), tứ giác APCM là hình bình hành
\( \Rightarrow HP//IC,\;HP\) là đường trung bình của \(\Delta DIC\)
\( \Rightarrow \) H là trung điểm của ID
Có \(\Delta AID\) cân tại A, \(\Delta DIC\) vuông tại I nên \(AI = AD\,;\,\,IP = ID\)
\( \Rightarrow \Delta AIP = \Delta ADP\) hay \(AI \bot IP\).
Đường thẳng AI đi qua I và vuông góc với IP nên ta có hệ phương trình: \(\begin{array}{l}\left\{ \begin{array}{l}x = 5 + 7t\\y = 2 - t\end{array} \right..\\IP = \left| {\overrightarrow {IP} } \right| = \frac{{5\sqrt 2 }}{2}.\end{array}\)
Gọi \(A\left( {5 + 7t;2 - t} \right)\). Vì \(AI = 2IP \Leftrightarrow A{I^2} = {\left( {5\sqrt 2 } \right)^2}\)
\( \Leftrightarrow 49{t^2} + {t^2} = 50 \Leftrightarrow {t^2} = 1 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = - 1\end{array} \right. \Rightarrow \left[ \begin{array}{l}A\left( {12;\;1} \right)\\A\left( { - 2;\;3} \right)\end{array} \right.\)
Do A có hoành độ âm nên \(t = - 1 \Rightarrow A\left( { - 2;3} \right)\)
\( \Rightarrow \overrightarrow {AP} = \left( {\frac{{15}}{2};\;\frac{5}{2}} \right) = \frac{5}{2}\left( {3;\;1} \right).\)
Đường thẳng AP có phương trình: \(x + 2 - 3\left( {y - 3} \right) = 0 \Leftrightarrow x - 3y + 11 = 0.\)
Đường thẳng DN đi qua \(I\) và vuông góc với \(AP\) có phương trình:
\(3\left( {x - 5} \right) + y - 2 = 0 \Leftrightarrow 3x + y - 17 = 0\)
\(AP \cap DN = \left\{ H \right\} \Rightarrow \) tọa độ điểm \(H\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x - 3y + 11 = 0\\3x + y - 17 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4\\y = 5\end{array} \right. \Rightarrow H\left( {4;5} \right).\)
H là trung điểm của ID \( \Rightarrow D\left( {3;8} \right)\)
Vậy \(A\left( { - 2;3} \right),\,\,D\left( {3;8} \right)\)
Chọn D.