Phương pháp giải:

Cách 1: Sử dụng quy tắc vẽ đồ thị hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) để tìm số điểm cực trị của hàm số.

Cách 2: Tìm hàm số \(y = f\left( x \right)\) dựa vào đồ thị hàm số sau đó suy ra hình dáng của đồ thị hàm số \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) để tìm số điểm cực trị của hàm số.

Lời giải chi tiết:

Dựa vào đồ thị hàm số ta thấy hàm số có dạng: \(y = a{x^3} + b{x^2} + cx + d\,\,\,\left( {a \ne 0} \right)\)

Đồ thị hàm số đi qua các điểm \(\left( { - 2;\; - 1} \right),\;\;\left( { - 1;\;3} \right),\;\left( {1; - 1} \right),\;\left( {2;\;3} \right)\)

\( \Rightarrow \left\{ \begin{array}{l} - 1 =  - 8a + 4b - 2c + d\\3 =  - a + b - c + d\\ - 1 = a + b + c + d\\3 = 8a + 4b + 2c + d\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 0\\c =  - 3\\d = 1\end{array} \right. \Rightarrow y = {x^3} - 3x + 1.\)

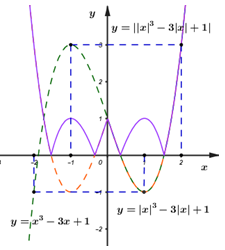
Khi đó ta có đồ thị hàm số \(y = \left| {\left| {{x^3}} \right| - 3\left| x \right| + 1} \right|\) như hình vẽ sau.

Dựa vào đồ thị hàm số ta thấy hàm số có 7 điểm cực trị.

Chọn B.