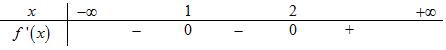Câu hỏi
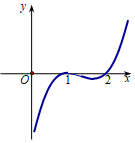
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\) có đồ thị của hàm số \(y = f'\left( x \right)\) như hình vẽ. Hỏi hàm số \(y = f\left( x \right)\) đồng biến trên khoảng nào dưới đây?
- A \(\left( {0;1} \right)\)
- B \(\left( {2; + \infty } \right)\)
- C \(\left( {1;2} \right)\)
- D \(\left( {0;1} \right)\) và \(\left( {2; + \infty } \right)\)
Phương pháp giải:
Lập BXD của \(f'\left( x \right)\) và kết luận các khoảng đơn điệu của hàm số.
Lời giải chi tiết:
Ta có BXD của \(f'\left( x \right)\) như sau :
Dựa vào BXD ta có :
Hàm số nghịch biến trên \(\left( { - \infty ;1} \right),\,\,\left( {1;2} \right)\) và đồng biến trên \(\left( {2; + \infty } \right)\).
Dựa vào đồ thị của hàm số \(y = f'\left( x \right)\) ta thấy \(f'\left( x \right)\)đồng biến trên khoảng \(\left( {2; + \infty } \right)\) \( \Rightarrow y = f\left( x \right)\) đồng biến trên \(\left( {2; + \infty } \right)\)
Chọn B.
Câu hỏi trước
