Câu hỏi
Cho hình lăng trụ ABC.A’B’C’ có thể tích là \(V\). Điểm M nằm trên cạnh AA’ sao cho AM = 2MA’. Gọi \(V'\) là thể tích của khối chóp M.BCC’B’. Tính tỉ số \(\dfrac{{V'}}{V}\) .
- A \(\dfrac{{V'}}{V} = \dfrac{1}{3}\)
- B \(\dfrac{{V'}}{V} = \dfrac{1}{2}\)
- C \(\dfrac{{V'}}{V} = \dfrac{3}{4}\)
- D \(\dfrac{{V'}}{V} = \dfrac{2}{3}\)
Phương pháp giải:
Nhận xét \({V_{M.BCC'B'}} = {V_{A.BCC'B'}}\).
Lời giải chi tiết:
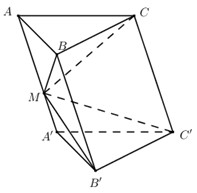
Ta có: \(AA'//\left( {BCC'B'} \right) \Rightarrow d\left( {M;\left( {BCC'B'} \right)} \right) = d\left( {A;\left( {BCC'B'} \right)} \right)\)
\( \Rightarrow {V_{M.BCC'B'}} = {V_{A.BCC'B'}} = \dfrac{{2V}}{3} \Rightarrow V' = \dfrac{{2V}}{3} \Rightarrow \dfrac{{V'}}{V} = \dfrac{2}{3}\).
Chọn D.
Câu hỏi trước
