Câu hỏi
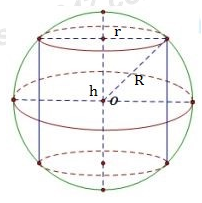
Chiều cao của khối trụ có thể tích lớn nhất nội tiếp trong hình cầu có bán kính \(R\) là
- A
\(\dfrac{{4R\sqrt 3 }}{3}\).
- B
\(R\sqrt 3 \).
- C
\(\dfrac{{R\sqrt 3 }}{3}\).
- D \(\dfrac{{2R\sqrt 3 }}{3}\).
Phương pháp giải:
Thể tích khối trụ: \(V = \pi {r^2}h\)
Công thức liên hệ: \({R^2} = {r^2} + {d^2}\), d là khoảng cách từ tâm O đến mặt đáy của hình trụ, r là bán kính đáy, R là bán kính mặt cầu.
Lời giải chi tiết:
Gọi d là khoảng cách từ tâm O đến mặt đáy của hình trụ, r là bán kính đáy.
Thể tích khối trụ: \({V_{tru}} = \pi {r^2}h\)
Mà \({R^2} = {r^2} + {d^2} \Rightarrow {R^2} = {r^2} + {\left( {\dfrac{h}{2}} \right)^2} \Rightarrow {r^2} = {R^2} - \dfrac{{{h^2}}}{4}\)
\( \Rightarrow {V_{tru}} = \pi {r^2}h = \pi \left( {{R^2} - \dfrac{{{h^2}}}{4}} \right)h = \dfrac{\pi }{4}\left( {4{R^2}h - {h^3}} \right)\)
Xét hàm số \(f\left( h \right) = 4{R^2}h - {h^3},\,\,\left( {0 < 0 < R} \right)\) có \(f'\left( h \right) = 4{R^2} - 3{h^2},\,\,f'\left( h \right) = 0 \Leftrightarrow h = \dfrac{{2R}}{{\sqrt 3 }}\)
Ta có: \(f\left( 0 \right) = 0,\,\,f\left( R \right) = 3{R^3},\,\,f\left( {\dfrac{{2R}}{{\sqrt 3 }}} \right) = {\dfrac{{16\sqrt 3 R}}{9}^3} \Rightarrow f{\left( h \right)_{\max }} = f\left( {\dfrac{{2R}}{{\sqrt 3 }}} \right)\)
Vậy, thể tích khối trụ lớn nhất khi \(h = \dfrac{{2R}}{{\sqrt 3 }} = \dfrac{{2R\sqrt 3 }}{3}\).
Chọn: D