Câu hỏi
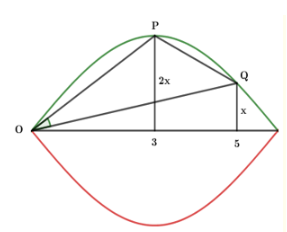
Trên một sợi dây đàn hồi đang có sóng dừng ổn định với bước sóng 12cm. Gọi O là một vị trí của một nút sóng, P, Q là hai phần tử trên dây cùng một bên so với O và có vị trí cân bằng cách O lần lượt là 3cm và 5cm. Tại thời điểm mà P có vận tốc bằng 0 thì góc POQ bằng 300. Giá trị lớn nhất của biên độ dao động điểm Q gần giá trị nào nhất sau đây?
- A 4,33cm
- B 10,54cm
- C 3,46cm
- D 5,27cm
Phương pháp giải:
Khoảng cách giữa nút và bụng liên tiếp là λ/4
Biên độ dao động của điểm cách nút sóng đoạn d là \(a=\left| 2A\sin \frac{2\pi d}{\lambda } \right|\)
Lời giải chi tiết:
O là nút, P và Q có VTCB cách O lần lượt 3cm và 5cm.
OP = 3cm = λ/4 --> P là điểm bụng
Biên độ dao động của Q là \({{A}_{Q}}=\left| 2A\sin \frac{2\pi d}{\lambda } \right|=\frac{{{A}_{b}}}{2}\)
Nếu đặt AQ là x thì AP = 2x
Khi P có vận tốc bằng 0 thì P đang ở biên. Mà P và Q cùng trên 1 bó sóng nên chúng dao động cùng pha, khi đó Q cũng ở biên.
Từ hình vẽ ta có : \(\tan {{30}^{0}}=\frac{\frac{2x}{3}-\frac{x}{5}}{1+\frac{2x}{3}.\frac{x}{5}}\)
--> x = 1,73cm hoặc x = 4,33cm
Chọn A