Câu hỏi
Một con lắc lò xo nằm ngang dao động theo phương trình x = 5cos(2πt - π/3)(cm) ( x tính bằng cm; t tính bằng s). Kể từ t = 0, lực đàn hồi đổi chiều lần đầu tại thời điểm
- A 2/3 s.
- B 11/12 s.
- C 1/6 s.
- D 5/12 s.
Phương pháp giải:
Sử dụng lí thuyết về lực đàn hồi trong dao động điều hòa của CLLX ngang và đường tròn lượng giác
Lời giải chi tiết:
+ Đối với CLLX ngang thì lực đàn hồi đổi chiều tại VTCB
+ Biểu diễn trên đường tròn lượng giác :
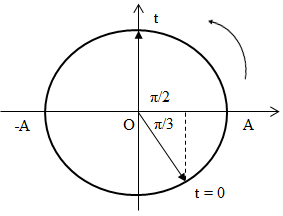
Góc quét được: \(\alpha = \frac{\pi }{3} + \frac{\pi }{2} = \frac{{5\pi }}{6}rad\)
=> Từ t = 0 thì vật đi qua VTCB lần đầu tại thời điểm: \(t = \frac{\alpha }{\omega } = \frac{{5\pi }}{6}.\frac{1}{{2\pi }} = \frac{5}{{12}}s\)
Câu hỏi trước
