Câu hỏi
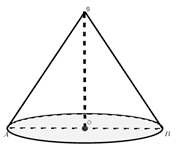
Thiết diện qua trục của hình nón tròn xoay là một tam giác đều cạnh \(2a.\) Tính thể tích \(V\) của khối nón đó.
- A \(V = \pi {a^3}\sqrt 3 \)
- B \(V = \frac{{\pi {a^3}\sqrt 3 }}{3}\)
- C \(V = \frac{{\pi {a^3}\sqrt 3 }}{{24}}\)
- D \(V = \frac{{3\pi {a^3}}}{8}\)
Phương pháp giải:
Sử dụng công thức tính thể tích khối nón \(V = \frac{1}{3}\pi {r^2}h\) với \(r\) là bán kính đáy, \(h\) là chiều cao hình nón
Lời giải chi tiết:
Cắt hình nón bằng mặt phẳng qua trục ta dược thiết diện là tam giác đều \(SAB\) có cạnh \(AB = 2r = 2a \Rightarrow R = a\) và trung tuyến \(SO = \frac{{a\sqrt 3 }}{2}.\)
Thể tích khối nón là \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {a^2}.a\sqrt 3 = \frac{{\pi {a^3}\sqrt 3 }}{3}\) .
Chọn B.
Câu hỏi trước
