Lời giải chi tiết:

Nhận xét:
Để tổng các số trong mỗi hàng và tổng các số trong mỗi cột đều bằng 0 thì số lượng số 1 và số lượng số -1 trong mỗi hàng và mỗi cột đều là 2.
\( \Leftrightarrow \) Mỗi hàng và mỗi cột đều có đúng 2 số 1.
- Chọn 2 ô ở cột 1 để đặt số 1, ta có: \(C_4^2 = 6\) (cách)
Ví dụ:

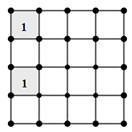
- Ở mỗi hàng mà chứa 2 ô vừa được chọn, ta chọn đúng 1 ô để đặt số 1, khi đó có 2 trường hợp:

TH1: 2 ô được chọn ở cùng một hàng: có \(C_3^1 = 3\) (cách)

Ví dụ:

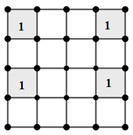
Khi đó, ở 2 hàng còn lại có duy nhất cách đặt số 1 vào 4 ô : không cùng hàng và cột với các ô đã điền.

Như hình vẽ sau:

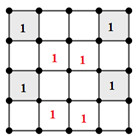
TH2: 2 ô được chọn khác hàng: có: \(3.2 = 6\) (cách)

Ví dụ:

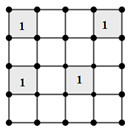
Khi đó, số cách đặt 4 số 1 còn lại là: \(1.1.2! = 2\) (cách), trong đó, 2 số 1 để vào đúng 2 ô còn lại của cột chưa điền, 2 số 1 còn lại hoàn vị vào 2 ô ở 2 cột vừa điền ở bước trước.

Ví dụ:

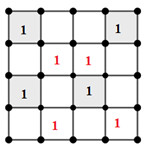
Vậy, số cách xếp là: \(6.\left( {3.1 + 6.2} \right) = 6.15 = 90\) (cách).

Chọn: B