Câu hỏi
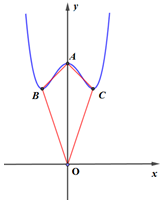
Gọi S là tập hợp tất cả các giá trị của tham số \(m\) đồ thị \((C)\) của hàm số \(y = {x^4} - 2{m^2}{x^2} + {m^4} + 5\) có ba cực trị, đồng thời ba điểm cực trị với gốc tọa độ tạo thành một tứ giác nội tiếp. Tìm số phần tử của \(S.\)
- A 3
- B 2
- C 1
- D 0
Phương pháp giải:
Sử dụng dấu hiệu nhận biết của tứ giác nội tiếp.
Lời giải chi tiết:
Ta có: \(y = {x^4} - 2{m^2}{x^2} + {m^4} + 5 \Rightarrow y' = 4{x^3} - 4{m^2}x \Rightarrow y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = m\\x = - m\end{array} \right.\)
Để đồ thị hàm số có 3 điểm cực trị thì \(m \ne 0\).
Khi đó, tọa độ ba điểm cực trị là: \(A\left( {0;{m^4} + 5} \right),\,\,B\left( { - m;5} \right),\,C\left( {m;5} \right)\)
Dễ dàng chứng minh: \(\Delta ABO = \Delta ACO\,\, \Rightarrow \angle B = \angle C\)
Mà tứ giác \(ABOC\) nội tiếp, nên \(\angle B + \angle C = 180^\circ \Rightarrow \angle B = \angle C = 90^\circ \)
Khi đó, \(\overrightarrow {AB} .\overrightarrow {OB} = 0 \Leftrightarrow \left( { - m} \right).\left( { - m} \right) + \left( { - {m^4}} \right).5 = 0 \)
\(\Leftrightarrow - 5{m^4} + {m^2} = 0 \Leftrightarrow {m^2}\left( {1 - 5{m^2}} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\,\,(ktm)\\m = \pm \frac{1}{{\sqrt 5 }}\,\,(tm)\end{array} \right.\)
Vậy tập hợp S tất cả các giá trị của tham số m thỏa mãn yêu cầu đề bài có 2 phần tử là \( \pm \frac{1}{{\sqrt 5 }}\).
Chọn: B