Câu hỏi
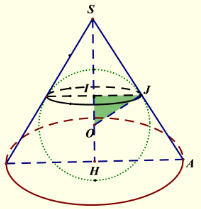
Cho một miếng tôn hình tròn có bán kính 70cm. Biết hình nón có thể tích lớn nhất khi diện tích toàn phần của hình nón bằng diện tích miếng tôn ở trên. Khi đó hình nón có bán kính đáy là:
- A \(40cm\).
- B \(10\sqrt 2 cm\).
- C \(70\sqrt 2 cm\).
- D \(35cm\).
Phương pháp giải:
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rl\)
Diện tích toàn phần của hình nón: \({S_{tp}} = \pi rl + \pi {r^2}\)
Lời giải chi tiết:
Miếng tôn hình tròn có diện tích: \(\pi {.70^2} = 4900\pi \left( {c{m^2}} \right)\)
Gọi bán kính đáy và chiều cao của hình nón lần lượt là \(r,\;h\;\;\left( {r,\;h > 0} \right).\)
Khi đó ta có: \(SA = \sqrt {{r^2} + {h^2}} .\)
\( \Rightarrow \) Diện tích toàn phần của hình nón là: \({S_{tp}} = \pi {r^2} + \pi r\sqrt {{r^2} + {h^2}} .\)
Theo đề bài ta có phương trình:
\(\begin{array}{l}\pi {r^2} + \pi r\sqrt {{r^2} + {h^2}} = 4900\pi \Leftrightarrow r\sqrt {{r^2} + {h^2}} = 4900 - {r^2}\\ \Leftrightarrow {r^2}\left( {{r^2} + {h^2}} \right) = {4900^2} - 2.4900{r^2} + {r^4} \Leftrightarrow {r^2} = \frac{{{{4900}^2}}}{{{h^2} + 9800}}\end{array}\)
Thể tích của khối nón là: \(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .\frac{{{{4900}^2}}}{{{h^2} + 9800}}.h = \frac{{{{4900}^2}\pi }}{3}.\frac{h}{{{h^2} + 9800}}\)
\( \Rightarrow V\) đạt Max \( \Leftrightarrow f'\left( h \right) = \frac{{{h^2} + 9800}}{h}\) đạt Min.
Ta có: \(f'\left( h \right) = \frac{{2{h^2} - {h^2} - 9800}}{{{h^2}}} = \frac{{{h^2} - 9800}}{{{h^2}}}.\)
\(\begin{array}{l} \Rightarrow f'\left( h \right) = 0 \Leftrightarrow {h^2} = 9800 \Leftrightarrow h = 70\sqrt 2 \;cm.\\ \Rightarrow {r^2} = \frac{{{{4900}^2}}}{{{h^2} + 9800}} = \frac{{{{4900}^2}}}{{9800.2}} = 1225\;cm\\ \Rightarrow r = \sqrt {1225} = 35\;cm.\end{array}\)
Vậy, hình nón có bán kính đáy là: \(35cm\).
Chọn: D