Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Phương trình \(2f\left( x \right) - 5 = 0\) có bao nhiêu nghiệm âm?
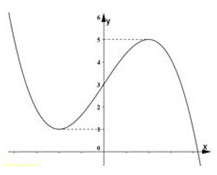
- A \(0\)
- B \(2\)
- C \(1\)
- D \(3\)
Phương pháp giải:
Tìm giao điểm của đường thẳng \(y = \dfrac{5}{2}\) với đồ thị hàm số và nhận xét tính chất nghiệm.
Lời giải chi tiết:
Ta có: \(2f\left( x \right) - 5 = 0 \Leftrightarrow f\left( x \right) = \dfrac{5}{2}\).
Nghiệm của phương trình chính là hoành độ giao điểm của đường thẳng \(y = \dfrac{5}{2}\) với đồ thị hàm số \(y = f\left( x \right)\).
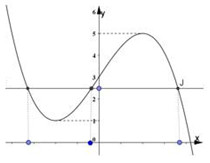
Quan sát đồ thị ta thấy đường thẳng \(y = \dfrac{5}{2}\) cắt đồ thị hàm số tại \(3\) điểm phân biệt, trong đó có \(2\) điểm có hoành độ âm và \(1\) điểm có hoành độ dương.
Vậy phương trình có \(2\) nghiệm âm.
Chọn B.







