Câu hỏi
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left[ { - 3;2} \right]\) và có bảng biến thiên như sau. Gọi \(M,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 1;2} \right]\). Tính \(M + m\).
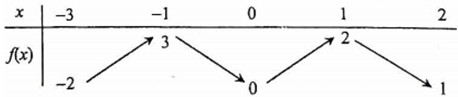
- A \(3\)
- B \(2\)
- C \(1\)
- D \(4\)
Phương pháp giải:
Quan sát bảng biến thiên và tìm GTLN, GTNN của hàm số trên đoạn \(\left[ { - 1;2} \right]\) rồi kết luận.
Lời giải chi tiết:
Quan sát bảng biến thiên ta thấy trên đoạn \(\left[ { - 1;2} \right]\) thì hàm số đạt GTNN bằng \(0\) tại \(x = 0\) và đạt GTLN bằng \(3\) tại \(x = - 1\).
Do đó \(M = 3;\,\,m = 0 \Rightarrow M + m = 3 + 0 = 3\).
Chọn A.
Câu hỏi trước
