Câu hỏi
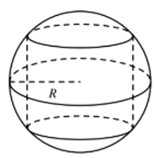
Thể tích lớn nhất của khối trụ nội tiếp hình cầu có bán kính \(R\) bằng:
- A \(\dfrac{{8\pi {R^3}\sqrt 3 }}{9}\)
- B \(\dfrac{{8\pi {R^3}\sqrt 3 }}{3}\)
- C \(\dfrac{{8\pi {R^3}}}{{27}}\)
- D \(\dfrac{{4\pi {R^3}\sqrt 3 }}{9}\)
Phương pháp giải:
+) Gọi \(h,\,r\) lần lượt là chiều cao và bán kính đáy của hình trụ.
+) Biểu diễn \(h\) theo \(R,\,\,r\).
+) Sử dụng công thức tính thể tích khối trụ là \(V = \pi {r^2}h\).
+) Sử dụng BĐT Cô-si cho ba số không âm \(\sqrt[3]{{abc}} \le \dfrac{{a + b + c}}{3}\).
Lời giải chi tiết:
Gọi \(h,\,r\) lần lượt là chiều cao và bán kính đáy của hình trụ.
Áp dụng định lí Pytago ta có : \(h = 2\sqrt {{R^2} - {r^2}} \)
Khi đó ta có thể tích khối trụ là \(V = \pi {r^2}h = 2\pi {r^2}\sqrt {{R^2} - {r^2}} = \sqrt 2 \pi \sqrt {{r^4}\left( {{R^2} - {r^2}} \right)} = \sqrt {{r^2}.{r^2}\left( {2{R^2} - 2{r^2}} \right)} \)
Áp dụng BĐT Cô-si ta có : \(\sqrt[3]{{{r^2}.{r^2}\left( {2{R^2} - 2{r^2}} \right)}} \le \dfrac{{{r^2} + {r^2} + \left( {2{R^2} - 2{r^2}} \right)}}{3} = \dfrac{{2{R^2}}}{3} \Rightarrow {r^2}.{r^2}\left( {2{R^2} - 2{r^2}} \right) = \dfrac{{8{R^6}}}{{27}}\)
\( \Rightarrow V \le \sqrt 2 \pi \sqrt {\dfrac{8}{{27}}{R^6}} = \dfrac{{4\pi \sqrt 3 {R^3}}}{9}\). Dấu "=" xảy ra \( \Leftrightarrow {r^2} = 2{R^2} - 2{r^2} \Leftrightarrow r = \dfrac{2}{3}R \Rightarrow \dfrac{{R\sqrt 6 }}{3}\).
Chọn D.







