Câu hỏi
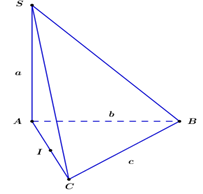
Trong không gian, cho hình chóp \(S.ABC\) có \(SA,AB,BC\) đôi một vuông góc với nhau và \(SA = a,SB = b,SC = c.\) Mặt cầu đi qua \(S,A,B,C\) có bán kính bằng
- A \(\frac{{2\left( {a + b + c} \right)}}{3}\)
- B \(\sqrt {{a^2} + {b^2} + {c^2}} \)
- C \(2\sqrt {{a^2} + {b^2} + {c^2}} \)
- D \(\frac{1}{2}\sqrt {{a^2} + {b^2} + {c^2}} \)
Phương pháp giải:
Sử dụng công thức tính bán kính mặt cầu ngoại tiếp khối chóp có cạnh bên vuông góc với mặt đáy:
\(R = \sqrt {{{\left( {\frac{h}{2}} \right)}^2} + {r^2}} \) với \(h\) là độ dài cạnh bên vuông góc với mặt đáy và \(r\) là bán kính đường tròn ngoại tiếp đa giác đáy.
Lời giải chi tiết:
Ta có: \(SA,\;AB,\;BC\) đôi một vuông góc
\( \Rightarrow SA \bot \left( {ABC} \right)\) và \(\Delta ABC\) vuông tại \(B.\)
Gọi \(I\) là trung điểm của \(AC \Rightarrow I\) là tâm đường tròn ngoại tiếp \(\Delta ABC.\)
Khi đó bán kính đường tròn tâm \(I\) ngoại tiếp \(\Delta ABC:\) \(r = \frac{1}{2}AC = \frac{1}{2}\sqrt {{b^2} + {a^2}} .\)
Khi đó bán kính mặt cầu ngoại tiếp hình chóp \(SABC\) là:
\(R = \sqrt {{{\left( {\frac{{SA}}{2}} \right)}^2} + {r^2}} = \sqrt {\frac{{{a^2}}}{4} + \frac{{{b^2} + {c^2}}}{4}} = \frac{1}{2}\sqrt {{a^2} + {b^2} + {c^2}} .\)
Chọn D.