Câu hỏi
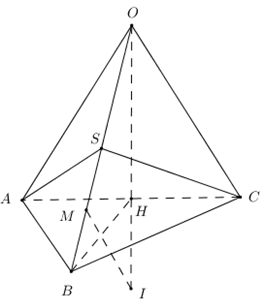
Cho hình chóp O.ABC có OA = OB = OC = a, \(\angle {\rm{AOB}} = {60^0},\angle {\rm{BOC}} = {90^0},\angle {\rm{COA}} = {120^0}.\) Gọi S là trung điểm của OB. Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là
- A \(\frac{a}{4}\)
- B \(\frac{{a\sqrt 7 }}{4}\)
- C \(\frac{{a\sqrt 7 }}{2}\)
- D \(\frac{a}{2}\)
Lời giải chi tiết:
\(\Delta OAB\) đều \( \Rightarrow AB = OA = OB = a\)
Áp dụng định lí Pytago trong tam giác vuông \(OBC\) ta có: \(BC = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \).
Áp dụng định lí Cosin trong tam giác \(OAC\) ta có
\(AC = \sqrt {O{A^2} + O{C^2} - 2OA.OC.\cos {{120}^0}} = \sqrt {{a^2} + {a^2} - 2{a^2}.\frac{{ - 1}}{2}} = a\sqrt 3 \)
Xét tam giác \(ABC\) ta có: \(A{B^2} + B{C^2} = A{C^2} \Rightarrow \Delta ABC\) vuông tại B.
Gọi H là trung điểm của \(AC \Rightarrow H\) là tâm đường tròn ngoại tiếp tam giác \(ABC\).
Mà \(OA = OB = OC \Rightarrow OH \bot \left( {ABC} \right) \Rightarrow OH\) là trục của tam giác \(ABC\).
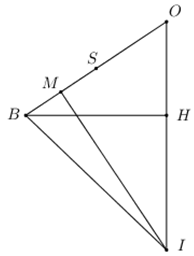
Gọi M là trung điểm của SB, trong \(\left( {SBH} \right)\) kẻ đường thẳng vuông góc với SB cắt OH tại I.
Ta có \(I \in OH \Rightarrow IA = IB = IC\).
Lại có \(IS = IB \Rightarrow IA = IB = IC = IS \Rightarrow I\) là tâm mặt cầu ngoại tiếp chóp \(S.ABC\).
Ta có: \(OH = \sqrt {O{A^2} - A{H^2}} = \sqrt {{a^2} - \frac{{3{a^2}}}{4}} = \frac{a}{2}\).
\(\begin{array}{l}BH = \frac{1}{2}AC = \frac{{a\sqrt 3 }}{2}\\ \Rightarrow OB = \sqrt {O{H^2} + B{H^2}} = \sqrt {\frac{{{a^2}}}{4} + \frac{{3{a^2}}}{4}} = a \Rightarrow BM = \frac{1}{4}OB = \frac{a}{4};\,\,OM = \frac{{3a}}{4}\\\Delta OBH \sim \Delta OIM\,\,\left( {g.g} \right) \Rightarrow \frac{{BH}}{{IM}} = \frac{{OH}}{{OM}} \Rightarrow IM = \frac{{\frac{{a\sqrt 3 }}{2}.\frac{{3a}}{4}}}{{\frac{a}{2}}} = \frac{{3a\sqrt 3 }}{4}\\ \Rightarrow IB = \sqrt {I{M^2} + B{M^2}} = \sqrt {\frac{{27{a^2}}}{{16}} + \frac{{{a^2}}}{{16}}} = \frac{{a\sqrt 7 }}{2}\end{array}\)
Chọn C.