Câu hỏi
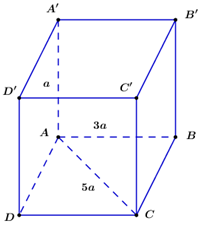
Cho khối hộp chữ nhật ABCD.A’B’C’D’ có \(AA' = a\,;\,\,AB = 3a\,;\,\,AC = 5a.\) Thể tích của khối hộp đã cho là
- A \(5{a^3}\)
- B \(4{a^3}\)
- C \(12{a^3}\)
- D \(15{a^3}\)
Phương pháp giải:
Áp dụng định lý Py-ta-go tính độ dài đoạn thẳng \(AD.\)
Thể tích hình hộp chữ nhật có các kích thước \(a,\;b,\;c:\;\;V = abc.\)
Lời giải chi tiết:
Ta có: \(AD = \sqrt {A{C^2} - C{D^2}} = \sqrt {{{25}^2} - 9{a^2}} = 4a.\) (định lý Pytago)
\({V_{ABCD.A'B'C'D'}} = AA'.AB.AD = a.3a.4a = 12{a^3}.\)
Chọn C.
Câu hỏi trước
