Câu hỏi
Cho mặt cầu \(\left( S \right)\) tâm \(I\) bán kính \(R.\,\,M\) là điểm thỏa mãn \(IM = \frac{{3R}}{2}.\) Hai mặt phẳng \(\left( P \right),\,\left( Q \right)\) qua \(M\) và tiếp xúc với \(\left( S \right)\) lần lượt tại \(A\) và \(B\) . Biết góc giữa \(\left( P \right)\) và \(\left( Q \right)\) bằng \({60^0}\) . Độ dài đoạn thẳng \(AB\) bằng
- A \(AB = R\)
- B \(AB = R\sqrt 3 \)
- C \(AB = \frac{{3R}}{2}\)
- D \(AB = R\) hoặc \(AB = R\sqrt 3 \)
Lời giải chi tiết:
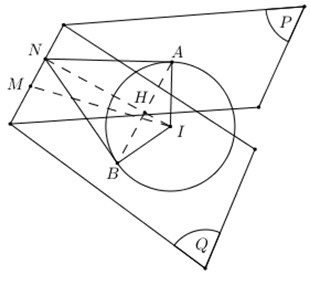
Gọi \(d=\left( P \right)\cap \left( Q \right)\). Kẻ \(IN\bot d\,\,\left( N\in d \right)\Rightarrow IN\le IM\).
Từ N kẻ hai tiếp tuyến NA, NB đến mặt cầu sao cho \(NA\bot d,\,\,NB\bot d\)
\(\Rightarrow \angle \left( \left( P \right);\left( Q \right) \right)=\angle \left( NA;NB \right)={{60}^{0}}\).
TH1: \(\angle ANB={{60}^{0}}\Rightarrow \angle ANI={{30}^{0}}\Rightarrow IN=\frac{AI}{\sin {{30}^{0}}}=2AI=2R>IM\).
TH2: \(\angle ANB={{120}^{0}}\Rightarrow \angle ANI={{60}^{0}}\Rightarrow \angle AIN={{30}^{0}}\).
Gọi H là trung điểm của AB ta có : \(IH\bot AB\).
Xét tam giác vuông IAN có: \(AH=AI.\sin {{30}^{0}}=\frac{R}{2}\Rightarrow AB=2AH=R\).
Chọn A.







