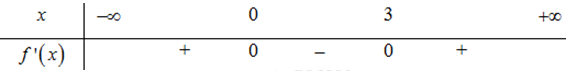Phương pháp giải:

Tính \(f'\left( x \right)\) và lập bảng xét dấu \(f'\left( x \right)\) từ đó kết luận các khoảng đơn điệu của hàm số.

Lời giải chi tiết:

TXĐ : \(D = \mathbb{R}\).

Ta có: \(f'\left( x \right) = \left( {{e^{\frac{1}{3}{x^3} - \frac{3}{2}{x^2}}}} \right)' = {e^{\frac{1}{3}{x^3} - \frac{3}{2}{x^2}}}\left( {\frac{1}{3}{x^3} - \frac{3}{2}{x^2}} \right)' = {e^{\frac{1}{3}{x^3} - \frac{3}{2}{x^2}}}.\left( {{x^2} - 3x} \right)\)

\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 3\end{array} \right.\)

Bảng xét dấu \(f'\left( x \right)\)

\( \Rightarrow \) Hàm số đồng biến trên \(\left( { - \infty ;0} \right)\) và \(\left( {3; + \infty } \right)\), hàm số nghịch biến trên \(\left( {0;3} \right)\).

Chọn B.