Phương pháp giải:

+) Tính y’, đặt \(t = \sin x\), xác định khoảng giá trị của t.

+) Xét phương trình \(y' = 0\), đưa phương trình về dạng \(f\left( t \right) = m\).

+) Hàm số ban đầu không có cực trị khi và chỉ khi phương trình \(f\left( t \right) = m\) vô nghiệm trên khoảng t đã xác định.

+) Lập BBT hàm số \(y = f\left( t \right)\) và kết luận.

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\).

Ta có:

\(\begin{array}{l}y' = 2\cos 2x - 4\sin x + m\sqrt 2  = 2\left( {1 - 2{{\sin }^2}x} \right) - 4\sin x + m\sqrt 2 \\\,\,\,\,\,\, =  - 4{\sin ^2}x - 4\sin x + 2 + m\sqrt 2 \end{array}\)

Đặt \(t = \sin x\), với \(x \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right] \Rightarrow t \in \left[ { - 1;1} \right]\)

Khi đó \(y' =  - 4{t^2} - 4t + 2 + m\sqrt 2 \,\,\forall t \in \left[ { - 1;1} \right]\)

Để hàm số không có cực trị trên \(\left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right] \Rightarrow \) Phương trình \(y' = 0\) không có nghiệm thuộc \(\left[ { - 1;1} \right]\).

Xét \(y' = 0 \Leftrightarrow  - 4{t^2} - 4t + 2 + m\sqrt 2  = 0\,\,\forall t \in \left[ { - 1;1} \right] \)

\(\Leftrightarrow m\sqrt 2  = 4{t^2} + 4t - 2\,\forall t \in \left[ { - 1;1} \right]\,\)

\( \Leftrightarrow m\sqrt 2  = f\left( t \right) = 4{t^2} + 4t - 2\,\forall t \in \left[ { - 1;1} \right]\,\).

Ta có \(f'\left( t \right) = 8t + 4 = 0 \Leftrightarrow t = \frac{{ - 1}}{2}\).

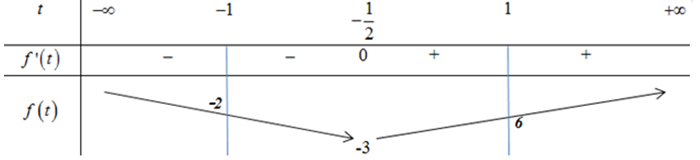
BBT:

Để phương trình không có nghiệm thuộc \(\left[ { - 1;1} \right] \Rightarrow \left[ \begin{array}{l}m\sqrt 2  <  - 3\\m\sqrt 2  > 6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < \frac{{ - 3}}{{\sqrt 2 }}\\m > 3\sqrt 2 \end{array} \right.\).

Kết hợp điều kiện đề bài \( \Rightarrow m \in \left\{ { - 5; - 4; - 3} \right\}\).

Chọn C.