Phương pháp giải:

Gọi \(M;N\) lần lượt là hình chiếu của \(A,B\) trên đáy còn lại không chứa \(A,B.\)

Từ đó ta sử dụng định lý Pytago để tìm cạnh của hình vuông

Sử dụng công thức: Diện tích hình vuông cạnh \(x\) bằng \({x^2}.\)

Lời giải chi tiết:

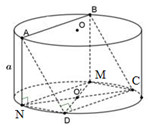
Xét hình trụ như trên. Gọi cạnh hình vuông \(ABCD\) là \(x\,\,\left( {x > 0} \right)\)

Gọi \(M;N\) lần lượt là hình chiếu của \(A,B\) trên đáy còn lại không chứa \(A,B.\)

Vì \(AB//DC;AB = DC \Rightarrow AB//MN//DC;AB = MN = DC\)  hay \(MNDC\) là hình bình hành tâm \(O'.\)

Lại có \(MD = NC = 2a\) nên \(MNDC\) là hình chữ nhật.

Suy ra \(ND = \sqrt {N{C^2} - D{C^2}}  = \sqrt {4{a^2} - {x^2}} \)  (1) (định lý Pytago trong tam giác \(DNC\))

Lại có tam giác \(AND\) vuông tại \(N\) nên theo định lý Pyatgo ta có \(ND = \sqrt {A{D^2} - A{N^2}}  = \sqrt {{x^2} - {a^2}} \)(2)

Từ (1) và (2) suy ra \(\sqrt {4{a^2} - {x^2}}  = \sqrt {{x^2} - {a^2}}  \Leftrightarrow 2{x^2} = 5{a^2} \Leftrightarrow x = \dfrac{{a\sqrt {10} }}{2}\)

Diện tich hình vuông \(ABCD\) là \({x^2} = {\left( {\dfrac{{a\sqrt {10} }}{2}} \right)^2} = \dfrac{{5{a^2}}}{2}.\) 

Chọn D.