Câu hỏi
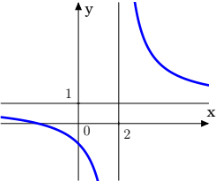
Đường cong trong hình bên là đồ thị của hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) với \(a,b,c,d\) là các số thực. Mệnh đề nào dưới đây đúng?
- A \(y' < 0,\forall x \ne 1\)
- B \(y' > 0,\forall x \ne 2\)
- C \(y' > 0,\forall x \ne 1\)
- D \(y' < 0,\forall x \ne 2\)
Phương pháp giải:
Quan sát và nhận xét dáng đồ thị hàm số, từ đó suy ra tính đồng biến nghịch biến và dấu của \(y'\).
Lời giải chi tiết:
Từ đồ thị hàm số ta thấy hàm số nghịch biến trên các khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
Vậy \(y' < 0,\forall x \ne 2\).
Chọn D.
Câu hỏi trước
