Phương pháp giải:

+) Dựng thiết diện \(MNPQ\,\,\left( {N \in AB,\,\,P \in AC,\,\,Q \in SC} \right)\).

+) \({V_1} = {V_{S.ANP}} + {V_{S.NPM}} + {V_{S.PMQ}}\)

+) Đặt \(\dfrac{{SM}}{{SB}} = x\). Sử dụng các công thức tỉ lệ thể tích, tính \({V_1}\) theo \(x\) và \(V\).

+) Dựa vào giả thiết \(\dfrac{{{V_1}}}{V} = \dfrac{{20}}{{27}}\) giải phương trình tìm \(x\).

Lời giải chi tiết:

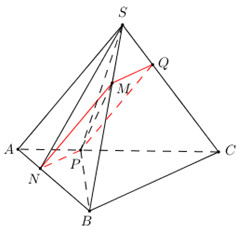
Dựng \(MN//SA\,\,\left( {N \in AB} \right),\,\,NP//BC\,\,\left( {P \in AC} \right);\,\,PQ//SA\,\,\left( {Q \in SC} \right)\).

Khi đó thiết diện cần tìm là \(MNPQ\).

Ta có \({V_1} = {V_{S.ANP}} + {V_{S.NPM}} + {V_{S.PMQ}}\)

Đặt \(\dfrac{{SM}}{{SB}} = x \Rightarrow \dfrac{{SQ}}{{SC}} = \dfrac{{AP}}{{AC}} = \dfrac{{AN}}{{AB}} = x\)

Ta có: 

\( \Rightarrow {V_1} = {V_{S.ANP}} + {V_{S.NPM}} + {V_{S.PMQ}} = \left( {{x^2} + 2{x^2}\left( {1 - x} \right)} \right)V \Rightarrow \dfrac{{{V_1}}}{V} = {x^2} + 2{x^2}\left( {1 - x} \right) = 3{x^2} - 2{x^3}\)

Mà  \(\dfrac{{{V_1}}}{V} = \dfrac{{20}}{{27}} \Leftrightarrow 3{x^2} - 2{x^3} = \dfrac{{20}}{{27}} \Leftrightarrow x = \dfrac{2}{3}\).

Chọn B.