Phương pháp giải:

+) Gọi \(G\) là trọng tâm tam giác \(BCD \Rightarrow AG \bot \left( {BCD} \right)\).

+) Áp dụng định lí Pytago tính \(AG\).

+) Tính thể tích \({V_{ABCD}} = \dfrac{1}{3}AG.{S_{BCD}}\).

Lời giải chi tiết:

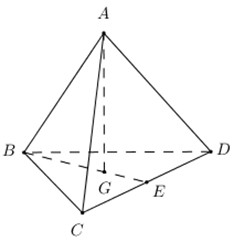
Gọi \(G\) là trọng tâm tam giác \(BCD \Rightarrow AG \bot \left( {BCD} \right)\).

Gọi \(E\) là trung điểm của \(CD\). Do \(BCD\) là tam giác đều cạnh \(2a \Rightarrow BE = \dfrac{{2a\sqrt 3 }}{2} = a\sqrt 3 \).

\( \Rightarrow BG = \dfrac{2}{3}BE = \dfrac{{2a\sqrt 3 }}{3}\).

Áp dụng định lí Pytago trong tam giác vuông \(ABG\) ta có : \(AG = \sqrt {A{B^2} - B{G^2}}  = \dfrac{{2a\sqrt 6 }}{3}\).

Tam giác \(BCD\) đều cạnh \(2a \Rightarrow {S_{BCD}} = \dfrac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 \).

Vậy  \({V_{ABCD}} = \dfrac{1}{3}AG.{S_{BCD}} = \dfrac{1}{3}.\dfrac{{2a\sqrt 6 }}{3}.{a^2}\sqrt 3  = \dfrac{{2{a^3}\sqrt 2 }}{3}\).

Chọn D.