Câu hỏi
Một sóng cơ lan truyền trên sợi dây theo chiều từ N đến M với chu kỳ T = 1,5s, biên độ không đổi. Ở thời điểm t0, li độ của phần tử tại M và N là -5mm, phần tử tại trung điểm P của MN đang ở vị trí biên dương. Thời điểm t1, li độ của các phần tử tại M và N tương ứng là -12mm và 12mm. Tại thời điểm t2 = t1 + 0,2s thì phần tử tại P cách vị trí cân bằng một khoảng gần nhất với giá trị nào sau đây ?
- A 9,5mm
- B 8,5mm
- C 10,5mm
- D 12mm
Phương pháp giải:
Vì P ở trung điểm MN nên khi xM = - xN thifP nằm ở VTCB
Vật đi từ biên ra VTCB hết thời gian T/4
Lời giải chi tiết:
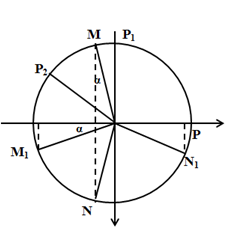
Ở thời điểm t1 xM và xN đối xứng nhau qua trục thẳng đứng nên P là trung điểm ở vị trí cân bằng như hình vẽ.
Vậy thời điểm t1 = T/4
Ta có : \({{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =\frac{{{5}^{2}}}{{{A}^{2}}}+\frac{{{12}^{2}}}{{{A}^{2}}}=1\Rightarrow A=13cm\)
Sau thời gian t2 = t1 + 0,2s = t1 + 2T/15 chất điểm P quay thêm góc 480
Li độ của P khi đó là xp = -A.cos420 = - 9,66cm
Vậy P cách VTCB 9,66cm
Chọn A