Phương pháp giải:

Xác định trục của khối chóp sau đó dựng đường thẳng trung trực của một cạnh bên của khối chóp để tìm được tâm của mặt cầu. Từ đó tính bán kính mặt cầu.

Lời giải chi tiết:

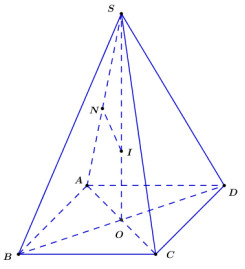
Gọi O là tâm của tứ giác đáy.

\( \Rightarrow \frac{1}{2}OA = \frac{1}{2}\sqrt {A{D^2} + A{B^2}}  = \frac{1}{2}\sqrt {8{a^2}}  = a\sqrt 2 .\)

Khi đó ta có: \(SO \bot \left( {ABCD} \right).\)

\( \Rightarrow SO\) là trục của đường tròn ngoại tiếp tứ giác ABCD.

Trong mặt phẳng \(\left( {SOA} \right),\) vẽ đường trung trực của cạnh \(SA,\) cắt \(SO\) tại \(I.\)

\( \Rightarrow I\) là tâm mặt cầu ngoại tiếp hình chóp.

Ta có: \(\Delta SNI \sim \Delta SOA\;\;\left( {g - g} \right)\)

\(\begin{array}{l} \Rightarrow \frac{{SN}}{{SO}} = \frac{{SI}}{{SA}} \Leftrightarrow SI = \frac{{SN.SA}}{{SO}}\\ \Leftrightarrow SI = \frac{{SN.SA}}{{\sqrt {S{A^2} - A{O^2}} }} = \frac{{2a.a}}{{\sqrt {4{a^2} - 2{a^2}} }} = \frac{{2{a^2}}}{{a\sqrt 2 }} = a\sqrt 2 .\end{array}\)  

Chọn B.