Câu hỏi
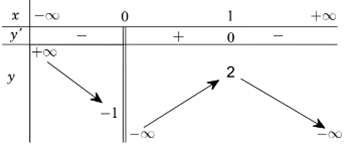
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
Tìm tất cả các giá trị thực của tham số \(m\) sao cho phương trình \(f\left( x \right) = m\) có đúng hai nghiệm.
- A \(m < - 1\), \(m = 2.\)
- B \(m \le - 1\), \(m = 2.\)
- C \(m \le 2.\)
- D \(m < 2.\)
Phương pháp giải:
Số nghiệm của phương trình \(f\left( x \right) = m\) bằng số giao điểm của đồ thị hàm số \(y = f\left( x \right)\) và đường thẳng \(y = m\).
Lời giải chi tiết:
Phương trình \(f\left( x \right) = m\) có đúng hai nghiệm
\( \Leftrightarrow \) Đồ thị hàm số \(y = f\left( x \right)\) cắt đường thẳng \(y = m\) tại 2 điểm phân biệt \( \Leftrightarrow \) \(\left[ \begin{array}{l}m \le - 1\\m = 2\end{array} \right.\).
Chọn B.