Phương pháp giải:

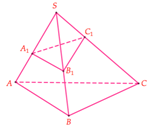
Cho khối chóp S.ABC, các điểm \({A_1},\,\;{B_1},\,\;{C_1}\) lần lượt thuộc \(SA,\,\;SB,\,\;SC\). Khi đó,

\(\frac{{{V_{S.\,{A_1}{B_1}{C_1}}}}}{{{V_{S.ABC}}}} = \frac{{S{A_1}}}{{SA}}.\frac{{S{B_1}}}{{SB}}.\frac{{S{C_1}}}{{SC}}\)

Lời giải chi tiết:

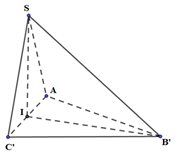
Trên các cạnh SB, SC lần lượt lấy B’, C’ sao cho \(SA = SB' = SC' = 2a\)

Khi đó, ta có: \(\frac{{{V_{S.ABC}}}}{{{V_{S.AB'C'}}}} = \frac{{SB}}{{SB'}}.\frac{{SC}}{{SC'}} = \frac{3}{2}.\frac{4}{2} = 3 \Rightarrow {V_{S.ABC}} = 3.{V_{S.AB'C'}}\)

* Tính \({V_{S.AB'C'}}\) (hình chóp \({V_{S.AB'C'}}\) có: \(SA = SB' = SC' = 2a\), \(\angle ASB' = \angle B'SC' = {60^0},\;\angle ASC = {90^0}\)):

\(\Delta ASB'\) và \(\Delta SB'C'\) đều, có cạnh bằng 2a \( \Rightarrow AB' = B'C' = 2a\)

\(\Delta SA'C'\) vuông cân tại S \( \Rightarrow \left\{ \begin{array}{l}A'C' = 2a\sqrt 2 \\{S_{AB'C'}} = \frac{1}{2}.{\left( {2a} \right)^2} = 2{a^2}\end{array} \right.\)

Do \(\left\{ \begin{array}{l}AB' = B'C' = 2a\\AC' = 2a\sqrt 2 \end{array} \right. \Rightarrow \Delta AB'C'\) vuông cân tại B’

Gọi I là trung điểm của A’C’ \( \Rightarrow I\) là tâm đường tròn ngoại tiếp tam giác AB’C’

Mà, chóp \({V_{S.AB'C'}}\) có \(SA = SB' = SC' = 2a \Rightarrow SI \bot \left( {AB'C'} \right)\)

\( \Rightarrow {V_{S.AB'C'}} = \frac{1}{3}{S_{AB'C'}}.SI = \frac{1}{3}.2{a^2}.\frac{{2a}}{{\sqrt 2 }} = \frac{{2\sqrt 2 {a^3}}}{3} \Rightarrow {V_{S.ABC}} = 3.{V_{S.AB'C'}} = 2\sqrt 2 {a^3}\).

Chọn B.