Phương pháp giải:

Sử dụng công thức tính thể tích lăng trụ \(V = h.S\) với \(h\) là chiều cao lăng trụ, \(S\) là diện tích đáy.

Tính diện tích các mặt cần sơn

Sử dụng bất đẳng thức Cô-si cho ba số không âm \(a;b;c\) ta có \(a + b + c \ge 3\sqrt[3]{{abc}}\)  để đánh giá.

Lời giải chi tiết:

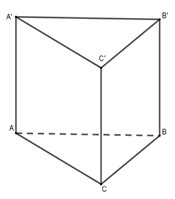
Gọi cạnh đáy lăng trụ là \(a;\) chiều cao lăng trụ là \(h\) ta có thể tích lăng trụ đều \(ABC.A'B'C'\) là

\(V = h.{S_{ABC}} = h.\dfrac{{{a^2}\sqrt 3 }}{4}\) . Theo gt ta có \(\dfrac{{{a^2}h\sqrt 3 }}{4} = \sqrt[4]{3} \Rightarrow h = \dfrac{4}{{{a^2}\sqrt[4]{3}}}\)

Diện tích hai mặt đáy và hai mặt bên cần sơn là

\(\begin{array}{l}S = 2{S_{ABC}} + 2{S_{AA'C'C}} = 2.\dfrac{{{a^2}\sqrt 3 }}{4} + 2.a.\dfrac{4}{{{a^2}\sqrt[4]{3}}}\\ = 2.\dfrac{{{a^2}\sqrt 3 }}{4} + 2.\dfrac{4}{{a\sqrt[4]{3}}} = 2\left( {\dfrac{{{a^2}\sqrt 3 }}{4} + \dfrac{2}{{a\sqrt[4]{3}}} + \dfrac{2}{{a\sqrt[4]{3}}}} \right)\\\mathop  \ge \limits^{Co  - si} 2.3\sqrt[3]{{\dfrac{{{a^2}\sqrt 3 }}{4}.\dfrac{2}{{a\sqrt[4]{3}}}.\dfrac{2}{{a\sqrt[4]{3}}}}} = 6\end{array}\)

Dấu “=” xảy ra khi \(\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{2}{{a\sqrt[4]{3}}} \Leftrightarrow a = \dfrac{2}{{\sqrt[4]{3}}}\) .

Chọn A.