Câu hỏi
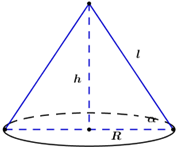
Cho hình nón có diện tích xung quanh bằng \(3\pi {a^2}\) và bán kính đáy bằng \(a.\) Tính tan của góc giữa một đường sinh và mặt đáy của nón.
- A \(3\)
- B \(\frac{{2\sqrt 2 }}{3}\)
- C \(2\sqrt 2 \)
- D \(\frac{1}{3}\)
Phương pháp giải:
Công thức tính diện tích xung quanh hình nón có bán kính đáy \(R,\;\) chiều cao \(h\) và đường sinh \(l:\;\;{S_{xq}} = \pi Rl.\)
Gọi \(\alpha \) là góc giữa đường sinh và mặt đáy của hình nón \( \Rightarrow \tan \alpha = \frac{h}{R} = \frac{{\sqrt {{l^2} - {R^2}} }}{R}\)
Lời giải chi tiết:
Ta có độ dài đường sinh của hình nón: \(l = \frac{{{S_{xq}}}}{{\pi R}} = \frac{{3\pi {a^2}}}{{\pi a}} = 3a.\)
\( \Rightarrow \tan \alpha = \frac{h}{R} = \frac{{\sqrt {{l^2} - {R^2}} }}{R} = \frac{{\sqrt {9{a^2} - {a^2}} }}{a} = 2\sqrt 2 .\)
Chọn C.
Câu hỏi trước
