Câu hỏi
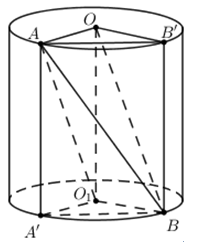
Cho hình trụ \(\left( T \right)\) có chiều cao bằng 2a. Hai đường tròn đáy của \(\left( T \right)\) có tâm lần lượt là O và \({O_1}\) và bán kính bằng a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn đáy tâm \({O_1}\) lấy điểm B sao cho \(AB = \sqrt 5 a\). Thể tích khối tứ diện \(O{O_1}AB\) bằng:
- A \(\frac{{\sqrt 3 {a^3}}}{{12}}\)
- B \(\frac{{\sqrt 3 {a^3}}}{4}\)
- C \(\frac{{\sqrt 3 {a^3}}}{6}\)
- D \(\frac{{\sqrt 3 {a^3}}}{3}\)
Phương pháp giải:
Trên \(\left( O \right)\) lấy điểm B’, trên \(\left( {{O_1}} \right)\) lấy điểm A’ sao cho \(AA'//BB'//O{O_1}\). Khi đó ta được hình lăng trụ \(OAB'.{O_1}A'B\). Dựa vào hình lăng trụ vừa dựng được, phân chia các khối đa diện và tính thể tích OO1AB.
Trên \(\left( O \right)\) lấy điểm B’, trên \(\left( {{O_1}} \right)\) lấy điểm A’ sao cho \(AA'//BB'//O{O_1}\). Khi đó ta được hình lăng trụ \(OAB'.{O_1}A'B\).
Ta có \(AA' = h = 2a,\,\,AB = a\sqrt 5 \).
Xét tam giác vuông AA’B có \(A'B = \sqrt {A{B^2} - AA{'^2}} = \sqrt {5{a^2} - 4{a^2}} = a\).
Do đó tam giác \({O_1}A'B\) có \({O_1}A' = {O_1}B = A'B = a \Rightarrow \Delta {O_1}A'B\) đều cạnh a \( \Rightarrow {S_{\Delta {O_1}A'B}} = \frac{{{a^2}\sqrt 3 }}{4}\).
\( \Rightarrow {V_{OAB'.{O_1}A'B}} = AA'.{S_{{O_1}A'B}} = 2a.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{2}\).
Ta có: \({V_{OAB'.{O_1}A'B}} = {V_{A.{O_1}A'B}} = {V_{OAB'.{O_1}A'B}} + {V_{B.OAB'}} + {V_{O{O_1}AB}}\)
Mà \({V_{A.{O_1}A'B}} = \frac{1}{3}{V_{OAB'.{O_1}A'B}};\,\,{V_{B.OAB'}} = \frac{1}{3}{V_{OAB'.{O_1}A'B}} \Rightarrow {V_{O{O_1}AB}} = \frac{1}{3}{V_{OAB'.{O_1}A'B}} = \frac{1}{3}.\frac{{{a^3}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{6}\)
Chọn C.
Lời giải chi tiết:
Trên \(\left( O \right)\) lấy điểm B’, trên \(\left( {{O_1}} \right)\) lấy điểm A’ sao cho \(AA'//BB'//O{O_1}\). Khi đó ta được hình lăng trụ \(OAB'.{O_1}A'B\).
Ta có \(AA' = h = 2a,\,\,AB = a\sqrt 5 \).
Xét tam giác vuông AA’B có \(A'B = \sqrt {A{B^2} - AA{'^2}} = \sqrt {5{a^2} - 4{a^2}} = a\).
Do đó tam giác \({O_1}A'B\) có \({O_1}A' = {O_1}B = A'B = a \Rightarrow \Delta {O_1}A'B\) đều cạnh a \( \Rightarrow {S_{\Delta {O_1}A'B}} = \frac{{{a^2}\sqrt 3 }}{4}\).
\( \Rightarrow {V_{OAB'.{O_1}A'B}} = AA'.{S_{{O_1}A'B}} = 2a.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{2}\).
Ta có: \({V_{OAB'.{O_1}A'B}} = {V_{A.{O_1}A'B}} = {V_{OAB'.{O_1}A'B}} + {V_{B.OAB'}} + {V_{O{O_1}AB}}\)
Mà \({V_{A.{O_1}A'B}} = \frac{1}{3}{V_{OAB'.{O_1}A'B}};\,\,{V_{B.OAB'}} = \frac{1}{3}{V_{OAB'.{O_1}A'B}} \Rightarrow {V_{O{O_1}AB}} = \frac{1}{3}{V_{OAB'.{O_1}A'B}} = \frac{1}{3}.\frac{{{a^3}\sqrt 3 }}{2} = \frac{{{a^3}\sqrt 3 }}{6}\)
Chọn C.