Câu hỏi
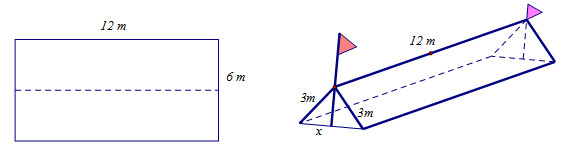
Trong một đợt tổ chức cho học sinh tham gia dã ngoại ngoài trời. Để có thể có chỗ nghỉ ngơi trong quá trình tham quan dã ngoại, các bạn học sinh đã dựng trên mặt đất bằng phẳng 1 chiếc lều bằng bạt từ một tấm bạt hình chữ nhật có chiều dài là \(12\,m\) và chiều rộng là \(6\,m\) bằng cách: Gập đôi tấm bạt lại theo đoạn nối trung điểm hai cạnh là chiều rộng của tấm bạt sao cho hai mép chiều dài còn lại của tấm bạt sát đất và cách nhau \(x\,(m)\) (xem hình vẽ). Tìm \(x\) để khoảng không gian phía trong lều là lớn nhất?
- A \(x = 3\sqrt 3 \)
- B \(x = 3\sqrt 2 \)
- C \(x = 2\)
- D \(x = 4\)
Phương pháp giải:
+ Xác định rằng không gian phía trong lều chính là thể tích hình lăng trụ.
+ Tính thể tích lều theo \(x\) .
+ Tìm \(x\) để hàm số đạt giá trị lớn nhất bằng cách sử dụng bất đẳng thức \(ab \le \dfrac{{{a^2} + {b^2}}}{2}\) hoặc dùng hàm số.
Lời giải chi tiết:
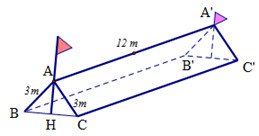
Gọi tên như hình vẽ với \(AH \bot BC \Rightarrow H\) là trung điểm của \(BC \Rightarrow BH = \dfrac{{BC}}{2} = \dfrac{x}{2}\)
Xét tam giác \(AHB\) vuông tại \(B,\) theo định lý \(AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{3^2} - \dfrac{{{x^2}}}{4}} = \dfrac{{\sqrt {36 - {x^2}} }}{2}\,\,\left( {0 < x < 6} \right)\)
\({V_{ABC.A'B'C'}} = {S_{ABC}}.AA' = \dfrac{1}{2}AH.BC.AA' = \dfrac{1}{2}\dfrac{{\sqrt {36 - {x^2}} }}{2}.x.12 = 3x\sqrt {36 - {x^2}} \)
Áp dụng bất đẳng thức \(ab \le \dfrac{{{a^2} + {b^2}}}{2}\) , ta có \(x\sqrt {36 - {x^2}} \le \dfrac{{{x^2} + 36 - {x^2}}}{2} \Leftrightarrow x\sqrt {36 - {x^2}} \le 18 \Leftrightarrow 3x\sqrt {36 - {x^2}} \le 54\)
Dấu “=” xảy ra khi \(x = \sqrt {36 - {x^2}} \Leftrightarrow 2{x^2} = 36 \Leftrightarrow \left[ \begin{array}{l}x = - 3\sqrt 2 \,\left( {ktm} \right)\\x = 3\sqrt 2 \,\,\,\,\left( {tm} \right)\end{array} \right.\)
Vậy \({V_{\max }} = 54 \Leftrightarrow x = 3\sqrt 2 .\)
Chọn: B







