Câu hỏi
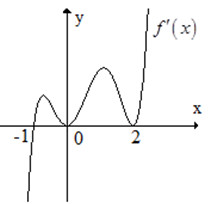
Hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) trên khoảng \({\rm{K}}\). Hình vẽ bên là đồ thị của hàm số \(f'\left( x \right)\) trên khoảng \({\rm{K}}\). Hỏi hàm số \(f\left( x \right)\) có bao nhiêu điểm cực trị?
- A 0
- B 4
- C 3
- D 1
Phương pháp giải:
Từ đồ thị hàm số của \(f'\left( x \right)\) ta lập bảng biến thiên, từ đó xác định điểm cực trị của hàm số.
Hoặc ta sử dụng cách đọc đồ thị hàm số \(f'\left( x \right)\)
Số giao điểm của đồ thị hàm số \(f'\left( x \right)\) với trục hoành bằng số điểm cực trị của hàm số \(f\left( x \right).\) (không tính các điểm tiếp xúc)
Nếu tính từ trái qua phải đồ thị hàm số \(f'\left( x \right)\) cắt trục hoành theo chiều từ trên xuống thì đó là điểm cực đại của hàm số \(f\left( x \right).\)
Nếu tính từ trái qua phải đồ thị hàm số \(f'\left( x \right)\) cắt trục hoành theo chiều từ trên xuống thì đó là điểm cực tiểu của hàm số \(f\left( x \right).\)
Lời giải chi tiết:
Từ đồ thị hàm số \(f'\left( x \right)\) ta thấy có một giao điểm với trục hoành (không tính điểm tiếp xúc) nên hàm số \(f\left( x \right)\) có một cực trị.
Chọn: D







