Câu hỏi
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên dưới:
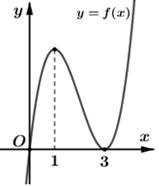
Tìm tất cả các giá trị của tham số \(m\) để đồ thị hàm số \(h\left( x \right) = \left| {{f^2}\left( x \right) + f\left( x \right) + m} \right|\) có đúng \(3\) điểm cực trị.
- A \(m \le 1\)
- B \(m > \dfrac{1}{4}\)
- C \(m < 1\)
- D \(m \ge \dfrac{1}{4}\)
Phương pháp giải:
- Xét \(g\left( x \right) = {f^2}\left( x \right) + f\left( x \right) + m\), lập bảng biến thiên tìm số cực trị của \(y = g\left( x \right)\).
- Tìm điều kiện để \(y = h\left( x \right) = \left| {g\left( x \right)} \right|\) có đúng \(3\) cực trị và kết luận.
Lời giải chi tiết:
Xét \(g\left( x \right) = {f^2}\left( x \right) + f\left( x \right) + m\) có \(g'\left( x \right) = 2f\left( x \right)f'\left( x \right) + f'\left( x \right) = f'\left( x \right)\left[ {2f\left( x \right) + 1} \right]\)
\(g'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}f'\left( x \right) = 0\\2f\left( x \right) + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\\x = a\left( {a < 0} \right)\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}g\left( 1 \right) = {f^2}\left( 1 \right) + f\left( 1 \right) + m\\g\left( 3 \right) = m\\g\left( a \right) = m - \dfrac{1}{4}\end{array} \right.\)
Bảng biến thiên của hàm số \(y = g\left( x \right)\)
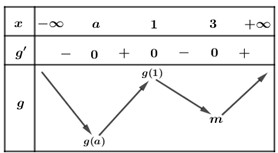
Dựa vào bảng biến thiên, suy ra đồ thị hàm số \(y = g\left( x \right)\) có \(3\) điểm cực trị.
Suy ra đồ thị hàm số \(h\left( x \right) = \left| {{f^2}\left( x \right) + f\left( x \right) + m} \right|\) có \(3\) điểm cực trị khi và chỉ khi đồ thị hàm số \(y = g\left( x \right)\) nằm hoàn toàn phía trên trục \(Ox\) (kể cả tiếp xúc)
Do đó \(g\left( a \right) \ge 0 \Leftrightarrow m - \dfrac{1}{4} \ge 0 \Leftrightarrow m \ge \dfrac{1}{4}\).
Chọn D.







