Phương pháp giải:

+ Sử dụng  định nghĩa để tìm góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) :

\(\left\{ \begin{array}{l}\left( P \right) \cap \left( Q \right) = d\\a \bot d;\,a \subset \left( P \right)\\b \bot d;b \subset \left( Q \right)\end{array} \right.\)  khi đó góc giữa \(\left( P \right)\) và \(\left( Q \right)\) chính là góc giữa hai đường thẳng \(a\) và \(b.\)

+ Diện tích tam giác đều cạnh \(a\) được tính theo công thức \(S = \dfrac{{{a^2}\sqrt 3 }}{4}\)

+ Tính thể tích \(V = \dfrac{1}{3}S.h\) với \(S\) là diện tích đáy, \(h\) là chiều cao hình chóp.

Lời giải chi tiết:

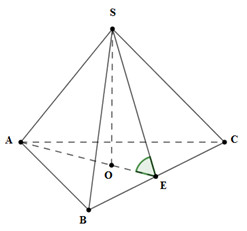
Gọi \(E\)  là trung điểm của \(BC,\,O\) là trọng tâm tam giác \(ABC \Rightarrow SO \bot \left( {ABC} \right)\)  (do \(S.ABC\) là hình chóp đều)

Suy ra \(AE \bot BC\,\)(do \(\Delta ABC\) đều) và \(SE \bot BC\) (do \(\Delta SBC\) cân tại \(S\) )

Ta có \(\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\AE \bot BC;AE \subset \left( {ABC} \right)\,\\SE \bot BC\,;SE \subset \left( {SBC} \right)\end{array} \right.\)  nên góc giữa \(\left( {ABC} \right)\) và \(\left( {SBC} \right)\) là \(\widehat {SEA}\) .

Từ giả thiết suy ra \(\widehat {SEA} = 60^\circ .\)

Tam giác \(ABC\) đều cạnh \(a \Rightarrow AE = \dfrac{{a\sqrt 3 }}{2} \Rightarrow OE = \dfrac{1}{3}AE = \dfrac{1}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}\)

Xét tam giác \(SOE\) vuông tại \(O\) (do \(SO \bot \left( {ABC} \right) \Rightarrow SO \bot AE\) ) , ta có: \(SO = OE.\tan \widehat {SEO} = \dfrac{{AE}}{3}.\tan {60^0} = \dfrac{{a\sqrt 3 }}{6}.\sqrt 3  = \dfrac{a}{2}.\)        

Diện tích tam giác đều \(ABC\) là: \({S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}.\)

Vậy \({V_{S.ABC}} = \dfrac{1}{3}{S_{\Delta ABC}}.SO = \dfrac{{{a^3}\sqrt 3 }}{{24}}.\)

Chọn: A