Câu hỏi
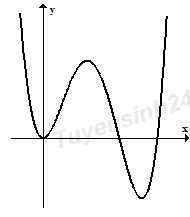
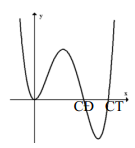
Cho hàm số \(y = f\left( x \right)\) có đạo hàm trên R và đồ thị hàm số \(y = f'\left( x \right)\) trên R như hình bên dưới. Khi đó trên R hàm số \(y = f\left( x \right)\)
- A có 1 điểm cực đại và 2 điểm cực tiểu.
- B có 1 điểm cực đại và 1 điểm cực tiểu.
- C có 2 điểm cực đại và 2 điểm cực tiểu.
- D có 2 điểm cực đại và 1 điểm cực tiểu.
Phương pháp giải:
Từ đồ thị hàm số của \(f'\left( x \right)\) ta lập bảng biến thiên, từ đó xác định điểm cực trị của hàm số.
Hoặc ta sử dụng cách đọc đồ thị hàm số \(f'\left( x \right)\)
Số giao điểm của đồ thị hàm số \(f'\left( x \right)\) với trục hoành bằng số điểm cực trị của hàm số \(f\left( x \right).\) (không tính các điểm tiếp xúc)
Nếu tính từ trái qua phải đồ thị hàm số \(f'\left( x \right)\) cắt trục hoành theo chiều từ trên xuống thì đó là điểm cực đại của hàm số \(f\left( x \right).\)
Nếu tính từ trái qua phải đồ thị hàm số \(f'\left( x \right)\) cắt trục hoành theo chiều từ trên xuống thì đó là điểm cực tiểu của hàm số \(f\left( x \right).\)
Lời giải chi tiết:
Từ đồ thị hàm số \(f'\left( x \right)\) ta thấy có hai giao điểm với trục hoành (không tính điểm tiếp xúc),trong đó tính từ trái qua phải một giao điểm cắt theo chiều từ trên xuống và một giao điểm cắt theo chiều từ dưới lên nên hàm số \(y = f\left( x \right)\) có một cực đại và một cực tiểu.
Chọn B.