Câu hỏi
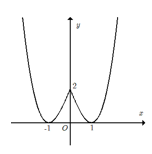
Cho hàm số \(y = f\left( x \right)\) liên tục trên R và có đồ thị như hình dưới đây.
(I). Hàm số nghịch biến trên khoảng \(\left( {0;1} \right)\).
(II). Hàm số đồng biến trên khoảng \(\left( { - 1;2} \right)\).
(III). Hàm số có ba điểm cực trị.
(IV). Hàm số có giá trị lớn nhất bằng \(2.\)
Số mệnh đề đúng trong các mệnh đề sau là:
- A 4
- B 2
- C 3
- D 1
Phương pháp giải:
Sử dụng cách đọc đồ thị hàm số.
Lời giải chi tiết:
Từ đồ thị hàm số ta thấy
+ Đồ thị đi xuống trên khoảng \(\left( {0;1} \right)\) nên Hàm số nghịch biến trên khoảng \(\left( {0;1} \right)\). Do đó (I) đúng
+ Đồ thị đi lên trên khoảng \(\left( { - 1;0} \right)\), đi xuống trên khoảng \(\left( {0;1} \right)\) và đi lên trên khoảng \(\left( {1;2} \right)\) nên trên khoảng \(\left( { - 1;2} \right)\) hàm số không hoàn toàn đồng biến. Do đó (II) sai.
+ Đồ thị hàm số có ba điểm hai điểm cực tiểu và một điểm cực đại nên (III) đúng.
+ Giá trị lớn nhất của hàm số là tung độ của điểm cao nhất của đồ thị hàm số nên (IV) sai.
Như vậy ta có hai mệnh đề đúng là (I) và (III).
Chọn B.