Câu hỏi
Cho hàm số \(y = \frac{{x + 1}}{{x - 1}}\) có đồ thị \(\left( C \right)\) biết cả hai đường thẳng \({d_1}:\;\;y = {a_1}x + {b_1};\;\;{d_2}:\;\;{a_2}x + {b_2}\) đi qua điểm \(I\left( {1;\;1} \right)\) và cắt đồ thị \(\left( C \right)\) tại 4 điểm tạo thành một hình chữ nhật. Khi \({a_1} + {a_2} = \frac{5}{2},\) giá trị biểu thức \(P = {b_1}{b_2}\) bằng:
- A \(\frac{5}{2}\)
- B \(\frac{1}{2}\)
- C \( - \frac{1}{2}\)
- D \( - \frac{5}{2}\)
Phương pháp giải:
Gọi \(\alpha ,\;\beta \) lần lượt là các góc tạo bởi tia \(Ox\) và phần đồ thị phía trên trục \(Ox\) của \({d_1},\;{d_2}.\)
Khi đó ta có: \({a_1} = \tan \alpha ,\;\;{a_2} = \tan \beta .\)
Lời giải chi tiết:
Gọi \(\alpha ,\;\beta \) lần lượt là các góc tạo bởi tia \(Ox\) và phần đồ thị phía trên trục \(Ox\) của \({d_1},\;{d_2}.\)
Khi đó ta có: \({a_1} = \tan \alpha ,\;\;{a_2} = \tan \beta .\)
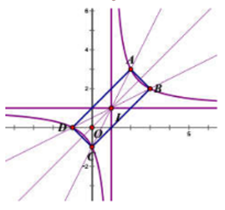
Vẽ đồ thị như hình vẽ bên.
Theo tính chất đối xứng của đồ thị hàm số ta có: \(\alpha + \beta = {90^0}\)
\( \Rightarrow {a_1} = \frac{1}{{{a_2}}}.\)
Lại có: \({a_1} + {a_2} = \frac{5}{2} \Rightarrow \Rightarrow \left\{ \begin{array}{l}{a_1} = 2\\{a_2} = \frac{1}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{b_1} = - 1\\{b_2} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow P = {b_1}{b_2} = - \frac{1}{2}.\)
Chọn C.