Câu hỏi
Một hình trụ có trục \(OO'\) chứa tâm của một mặt cầu bán kính \(R,\) các đường tròn đáy của hình trụ đều thuộc mặt cầu trên, đường cao của hình trụ bằng \(R.\) Tính thể tích \(V\) của khối trụ.
- A \(V = \frac{{3\pi {R^3}}}{4}\)
- B \(V = \pi {R^3}\)
- C \(V = \frac{{\pi {R^3}}}{4}\)
- D \(V = \frac{{\pi {R^3}}}{3}\)
Phương pháp giải:
Thể tích khối trụ có bán kính đáy \(R\) và chiều cao \(h\) là: \(V = \pi {R^2}h.\)
Lời giải chi tiết:
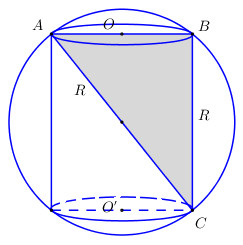
Áp dụng định lí Pytago trong tam giác vuông ABC ta có:
Đường kính đáy của khối trụ là: \(2r = \sqrt {{{\left( {2R} \right)}^2} - {R^2}} = R\sqrt 3 \Rightarrow r = \frac{{R\sqrt 3 }}{2}.\)
\( \Rightarrow V = \pi {r^2}h = \pi {\left( {\frac{{R\sqrt 3 }}{2}} \right)^2}R = \frac{{3\pi {R^3}}}{4}.\)
Chọn A.
Câu hỏi trước
